已知斜率k,一点坐标(a,b)和距离d,求另外一个点坐标(c,d)

假设这两条直线分别为l和m,已知的一点和垂足分别为点A和O,另一直线待求点为B,它到O点的距离为d
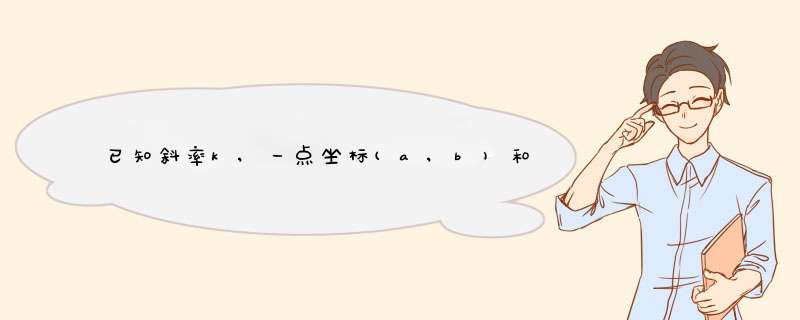
已知点A和O求出直线l的方程y1=ax+b,因为l和m垂直,由此可知m的斜率为-1/a,结合O点坐标求出直线m的方程为y2=-1/ax+c,设B（x,y）,将B带入直线m,再根据两点间的距离公式,求解,可知,符合条件的待求点有两个

已知斜率，则y=kx+b,,即kx+b-y=0
某点坐标（x,y)
点到直线的距离：d=|ax+by+c|除以√a^2+b^2
此式中，a=k，b=-1，c=b
带入d计算

以P1P2为斜边,点P1与点P2的横坐标差及纵坐标差为直角边,画出一个直角三角形
斜率是纵坐标差那边所对的角的正切值,
可以根据这个值求出相应的正弦sin a 或者余弦值cos a
sin a =纵坐标差/IP1P2I,cos a =横坐标差/IP1P2I
这就可求了……
根据余弦和正切或者正弦和正切的转换关系,就可以得出
IP1P2I=│x1-x2│√(k^2+1)=│y1-y2│√[(1/k^2)+1]
其中k为斜率,大小为tan a
补充一下转换关系 (k^2+1)=tan²a+1=sin²a/cos²a+1=(sin²a+cos²a)/cos²a=1/cos²a
IP1P2I=│x1-x2│√(k^2+1)=│x1-x2│√(1/cos²a)=(1/cosa)│x1-x2│
cosa=│x1-x2│/ IP1P2I

---