排列组合A几几的 C几几的怎么算比如A 3 2

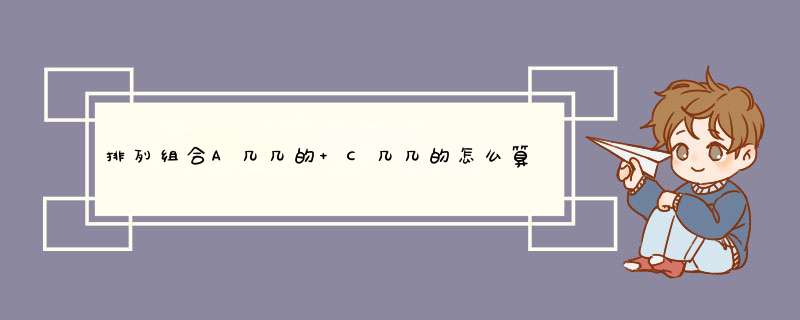
A(3，2)=3×2。

组合数学的重要概念之一。从n个不同元素中每次取出m个不同元素（0≤m≤n），不管其顺序合成一组，称为从n个元素中不重复地选取m个元素的一个组合。所有这样的组合的总数称为组合数，这个组合数的计算公式为

或者

n元集合A中不重复地抽取m个元素作成的一个组合实质上是A的一个m元子集合。

排列组合计算方法如下：

排列A(n,m)=n×（n-1）（n-m+1）=n!/（n-m）!(n为下标,m为上标,以下同)

组合C(n,m)=P(n,m)/P(m,m) =n!/m!（n-m）!；

例如：

A(4,2)=4!/2!=43=12

C(4,2)=4!/(2!2!)=43/(21)=6

A的：下面数字的阶乘除以上面数字的阶乘。例A下4上3的=4321/321
C的：下面数字的阶乘除以上面数字的阶乘再除以下面和上面的差的阶乘，
例C上2下5的= 54321/21/321

A上3下3是3的全排名，C上2下4是4选2的排列。

排列组合c的公式：C(n,m)=A(n,m)/m!=n!/m!（n-m）！与C(n,m)=C(n,n-m)。（n为下标，m为上标）。例如，C(4,2)=4!/(2!2!)=43/(21)=6；C(5,2)=C(5,3)。

排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。排列组合与古典概率论关系密切。

排列组合c的公式：C(n,m)=A(n,m)/m!=n!/m!（n-m）！与C(n,m)=C(n,n-m)。（n为下标，m为上标）。例如，C(4,2)=4!/(2!2!)=43/(21)=6；C(5,2)=C(5,3)。

排列组合c计算方法：C：指从几个中选取出来，不排列，只组合。C(n，m)=n(n-1)(n-m+1)/m!。例如c53=543÷(321)=10；再如C(4,2)=(4x3)/(2x1)=6。

计算概率组合C：从8个中任选3个：C上面写3下面写8，表示从8个元素中任取3个元素组成一组的方法个数，具体计算是：876/321；如果是8个当中取4个的组合就是：8765/4321。

---