怎么看增减函数

1、图象观察法
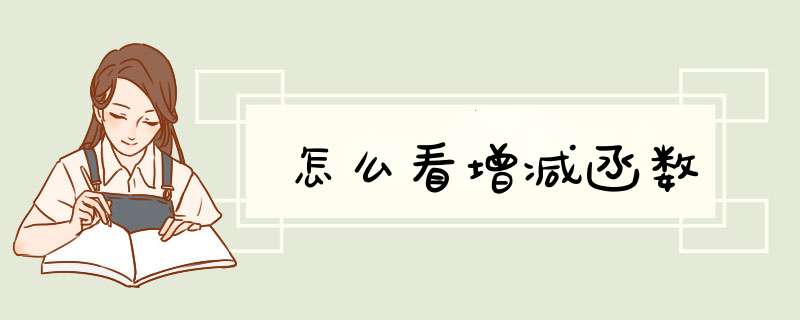
如上所述，在单调区间上，增函数的图象是上升的，减函数的图象是下降的。因此，在某一区间内，一直上升的函数图象对应的函数在该区间单调递增；一直下降的函数图象对应的函数在该区间单调递减。
2、求导法
导数与函数单调性密切相关。它是研究函数的另一种方法，为其开辟了许多新途径。特别是对于具体函数，利用导数求解函数单调性，思路清晰，步骤明确，既快捷又易于掌握，利用导数求解函数单调性，要求熟练掌握基本求导公式。
如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加；反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D内单调减少。

问题一：如何判断函数的增减性 楼上的哥们回答的是奇偶性。首先求这个函数的导数，当其导数大于零的区间，就是这个函数的增区间。其导数小于零的区间，就是这个函数的减区间。另一个方法是定义法，任取定义域中的x1，x2并且x1 问题二：如何快速判断一个函数的增减？？ 要看什么函数，方法一般有 作差，作除，求导等

问题三：如何快速判断一个函数是增函数还是减函数 可以先画出该函数的图像，在一个规定的区间内看Y值是随X的增大而减小还是随X的增大而增大。减小则为减函数，反之则为增函数。

问题四：怎么判断函数的增减性？ 方法一：求导，看导函数是否在该区间内大于0，大于0则函数为增，
小于0的区间则为递减区间
方法二：定义法，设x1 问题五：如何快速判断一个函数是增函数还是减函数。 利用复合函数的单调性！比如说：增函数乘以负数，就是减函数； 增函数减去减函数，还是增函数； 增函数的倒数，等等……很实用的！

问题六：如何判断函数的单调递增或递减？ （1）对函数求导得
f'(x)=0
解出x的值，x=C
（2）再根据x>C, x0, 函数为增区间
当f'(x)-2
f'(x)>0, 函数为增区间
。。。

问题七：怎样判断函数的增减性 判断函数单调性的常见方法
一、 函数单调性的定义：
一般的，设函数y=f(X)的定义域为A,IA，如对于区间内任意两个值X1、X2，
1）、当X1X2时，都有f(X1)>f(X2),那么就说y=f(x)在区间I上是单调减函数，I称为函数的单调减区间。
二、 常见方法： Ⅰ、定义法：
定义域判断函数单调性的步骤 ① 取值：
在函数定义域的某一子区间I内任取两个不等变量X1、X2，可设X1

证明函数的增减性有两种方法
1令任意的x1
f(x2)则是单调递减。2求导函数，通过讨论导函数的正负，从而得出函数的单调性和单调区间。3利用分析法（仅仅限于选择题或者填空题），一句话同增为增，同减为减。前两种是做大题时候要求过程的时候用的。而且前两种是最正规的。做选择题的时候，如果基础知识熟练，第三种方法很节省时间。

一般地,判断(而不是证明)函数的单调性,有下面几种方法1基本函数法用熟悉的基本函数（一次、二次、反比例、指数、对数、三角等函数）的单调性来判断函数单调性的方法叫基本函数法2图象法用函数图象来判断函数单调性的方法叫图象法图象从左往右逐渐上升是增函数图象从左往右逐渐下降是减函数3定义法用单调性的定义来判断函数的单调性的方法叫定义法设x1,x2∈D,x1)(x)是D上的增函数（减函数）过程为取值——作差——变形——判符号——结论其实,这也是单调性的证明过程4函数运算法用单调函数通过四则运算得到的和差积商函数来判断函数的单调性的方法叫函数运算法设f,g是增函数,则在f的单调增区间上,或者f与g的单调增区间的交集上,有如下结论：①f+g是增函数②－f是减函数③1/f
是减函数(f>0)④fg是增函数（f>0,且g>0）5导数法用导数符号来判断函数单调性的方法叫导数法f（x）是增函数(减函数)f′>0(f′

函数的定义域分为自身定义域和环境定义域。自身定义域就是使表达式有意义的定义域，比如说分式的分母不能为0，还有对数的自变量要大于0，还有正切函数的角度值不能取y轴上的角度值，余切函数的角度值不能取x轴上的角度值，环境定义域就是指在实际环境中的定义域，如在一个实际应用题中，要求某一个未知量的值，二而这个未知数具有一定的物理意义或数学意义时候，那么这时候这个未知量就必须满足其本身的要求。

答：
这4个都是要证明吗？还是作什么？
1）
f(x)=5x+7
设x1>x2
f(x1)-f(x2)=5x1+7-(5x2+7)=5(x1-x2)>0
f(x1)>f(x2)
所以：f(x)=5x+7是（-∞，+∞）上的增函数
2）
f(x)=5/x
设x1>x2>0
f(x1)-f(x2)
=5/x1-5/x2
=5(x2-x1)/(x1x2)
<0
f(x1)<f(x2)
所以：f(x)=5/x是(0，+∞）上的减函数
3）
f(x)=2x²-7
设x2<x1<0
f(x1)-f(x2)
=2x1²-7-(2x2²-7)
=2(x1-x2)(x1+x2)
<0
f(x1)<f(x2)
所以：f(x)=2x²-7在（-∞，0）上是减函数
4）
f(x)=-5/x
设x1>x2>0
f(x1)-f(x2)
=-5/x1+5/x2
=-5(x2-x1)/(x1x2)
=5(x1-x2)/(x1x2)
>0
f(x1)>f(x2)
所以：f(x)=-5/x是(0，+∞）上的增函数

---