【Q】排列组合例题

1 10本书里有4本自传B,6本小说N。需要从中拿4本，其中自传大于等于2 问：多少种？

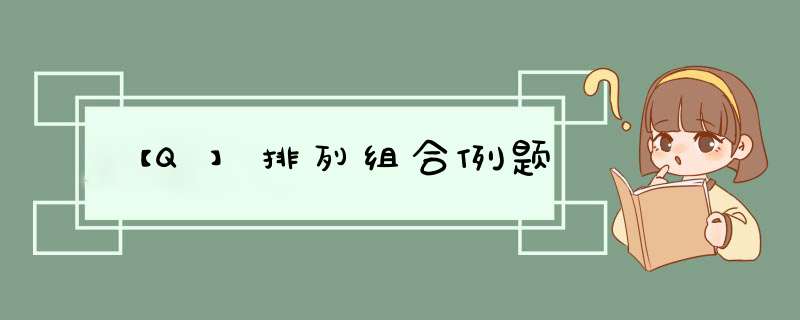
解：组合。公式m!/(n-m)!m!三种情况：

4B=1;

3B1N=4x3x2x6/ 3!x1!=24;  

2B2N=4x3x6x5/ 2!x2!=90

link= >1自己选，你自己要看走势图什么的或者凭借自己的感觉选号！这样是要耗费些时间和精力！
2机选，你就不用花费心思了！投注站投注机机选！电脑软件自己机选！
这里推荐电脑软件自己机选！我给你个理由：如果我们全部都去机选的话，每期销量35亿，那么就有投注125亿注了！
理论中二等奖的概率是180W分之一的概率！
按着这样计算，如果都是机选的话，那么中二等奖的数量，就肯定不止这么多注！
每期开二等奖的，数量都是2百多注左右！按理说，这是不可能的啊！
个人觉得，投注机的机选有初始的人工干预措施导致机选很多都是一样的投注！
要不能二等奖不会这么少的！（当然，这里是我个人的猜测了，没有实际的证据，呵呵，不认同的，请不要喷我！）
下面是我给你推荐的软件！
软件只是补助的作用，没有准不准的概念！
个人建议你下载:
1500W双色球软件
2双色球助手22(很强大)
以上都是免费软件，祝你好运！
软件只是补助的作用，没有准不准的概念！

概念介绍：

从n个不同元素中取出r(r≤n)个元素的所有组合的个数，叫做从n个不同元素中取出r个元素的组合数  表示为

2 说明

数学意义：

从20个不同元素中，任取0个元素的所有组合的数量。

3 组合的计算公式：

4 计算过程：

，r=0，n=20 代入公式

=20！/（0！（20-0）！）=20！/（0！20！）=1/0！=1

由1，2组成的都出现的n位数的个数记为R(n,2)
则R(n,2)=C(n,1)+C(n,2)++C(n,n-1)
由1，2，3组成的都出现的n位数的个数记为R(n,3)
则出现1个3的是C(n,1)R(n-1,2)
则出现2个3的是C(n,2)R(n-2,2)

则出现n-2个3的是C(n,n-2)R(2,2)
所以
R(n,3)=C(n,1)R(n-1,2)+C(n,2)R(n-2,2)++C(n,n-2)R(2,2)
由1，2，,k组成的都出现的n位数的个数记为R(n,k),则一般的递推公式是
R(n,k)=C(n,1)R(n-1,k-1)+C(n,2)R(n-2,k-1)++C(n,n-k+1)R(k-1,k-1)
递归计算出R(10,6),这个是绝对不重复的。
R(10,6)=16435440

所谓有无差异，其实是顺序的问题。
我把题目换个问法：
1、把 AAAAA, 111 分成三组，每组必须有一个数字
2、把 ABCDE, 111 分成三组，每组必须有一个数字
3、把 AAAAA, 123 分成三组，每组必须有一个数字
4、把 ABCDE, 123 分成三组，每组必须有一个数字
一题。
既然顺序都不重要，那么分成三组时，3组的A数量不能大于2组；2组的A数量不能大于1组。
AAAAA1 1 1 [1]
AAAA1 A1 1 [1]
AAA1 AA1 1, AAA1 A1 A1 [2]
AA1 AA1 A1 [1]
共5种。
二题。
做此题时必须考虑到：单独组内的顺序不重要，即有差异的信封放在同一个邮筒里的顺序无所谓 (AB1 = BA1)。
下文运算符c即计算器中的运算符nCr。
ABCDE1 1 1 [(5c5)(0c0)(0c0) = 1]
ABCD1 E1 1, [(5c4)(1c1)(0c0) = 5]
ABC1 DE1 1, ABC1 D1 E1, [(5c3)(2c2)(0c0) + (5c3)(2c1)(1c1) = 30]
AB1 CD1 E1, [(5c2)(3c2)(1c1) = 30]
共66种。
三题。
每个123可以有 3! = 3×2×1 = 6种不同的组合方法。
既然字母没有差异，那么三题的结果就是一题的结果乘以6。
AAAAA1 2 3, [1×6 = 6]
AAAA1 A2 3, [1×6 = 6]
AAA1 AA2 3, AAA1 A2 A3, [2×6 = 12]
AA1 AA2 A3, [1×6 = 6]
共30种。
四题。
既然数字和字母都有差异，那么四题的结果就是二题的结果乘以3!即乘以6。
ABCDE1 2 3, [1×6 = 6]
ABCD1 E2 3, [5×6 = 30]
ABC1 DE2 3, ABC1 D2 E3, [30×6 = 180]
AB1 CD2 E3, [30×6 = 180]
共396种。

第一问，就是排列问题，A(14)(12)=1413123
第二问，AB出现的次数，就是选出12个里面必然有AB，那就是剩下的12个字母里任意选10个，
即，C(12)(10)A(12)(12)=1211/212!

LZ好，“选元”（从n类个不同元素中每次取出m个元素）是排列和组合两个概念的共同属性，而“排序”（是否将取出的m个元素按照一定的顺序排成一列）是排列和组合两个概念的不同属性．
你根据以上的定义可以知道，排列和组合都是从一个大范围里面取东西，区别是排列取出东西要再按顺序排列，组合取出的东西相互间没有顺序关系
举个简单的例子，
1从20个人中选3个人，不同选发是？
这时用的是组合，因为取出3个人后，没有要求他们再按什么排列，也就是对他们的位置没有限定

2，从20个人里选3个，而后按身高由高到矮排队，有多少不同方法？
这时用排列，因为从20个人里选3个后，还要按高矮排列，这时题2比题1的不同之处，按高矮排，就说明，题目是对3个人的顺序是有限定，这时用排列

同理，按高矮排还可以改成按体重，视力，分数，等等等等

自我感觉学的时候你知道概念和会做题是两会事，因为题目中有很多技巧，光知道概念是没法做的
比如以下
一、合理分类与准确分步法

解含有约束条件的排列组合问题，应按元素性质进行分类，按事情发生的连续过程分步，作到分类标准明确，分步层次清楚，不重不漏。
例1 、五个人排成一排，其中甲不在排头，乙不在排尾，不同的排法有 （ ）
A．120种 B．96种 C．78种 D．72种
选C

二、正难反易转化法
对于一些生疏问题或直接求解较为复杂或较为困难问题，从正面入手情况较多，不易解决，这时可从反面入手，将其转化为一个简单问题来处理。
例2、 马路上有8只路灯，为节约用电又不影响正常的照明，可把其中的三只灯关掉，但不能同时关掉相邻的两只或三只，也不能关掉两端的灯，那么满足条件的关灯方法共有多少种？
分析： 关掉第1只灯的方法有6种，关第二只，第三只时需分类讨论，十分复杂。若从反面入手考虑，每一种关灯的方法对应着一种满足题设条件的亮灯与关灯的排列，于是问题转化为“在5只亮灯的6个空中插入3只暗灯”的问题。

三、混合问题“先选后排”
对于排列组合混合问题，可先选出元素，再排列。
例 3、 4个不同小球放入编号为1，2，3，4的四个盒中，恰有一空盒的方法有多少种？
因有一空盒，故必有一盒子放两球，他们是先选的，答案144

四、特殊元素“优先安排法”
对于带有特殊元素的排列组合问题，一般应先考虑特殊元素，再考虑其它元素。
例4、 用0，2，3，4，5，五个数字，组成没有重复数字的三位数，其中偶数共有（ ）。
A24个 B。30个 C。40个 D。60个
[分析]由于该三位数为偶数，故末尾数字必为偶数，又因为0不能排首位，故0就是其中的“特殊”元素，应该优先安排，按0排在末尾和0不排在末尾分两类 选B

五、总体淘汰法
对于含有否定字眼的问题，可以从总体中把不符合要求的除去，此时需注意不能多减，也不能少减。
例子4可以按这个方法做

六、局部问题“整体优先法”
对于局部排列问题，可先将局部看作一个元与其余元素一同排列，然后在进行局部排列。
例5、7人站成一排照相，要求甲乙两人之间恰好隔三人的站法有多少种？
分析： 甲、乙及间隔的3人组成一个“小整体”，这3人可从其余5人中选，这是第一步要做的 答案720

七、相邻问题一“元”法
对于某几个元素要求相邻的排列问题，可将相邻的元素看作一个“元”与其他元素排列，然后在对“元”内部元素排列。
例6、 7人站成一排照相，甲、乙、丙三人相邻，有多少种不同排法？
分析： 把甲、乙、丙三人看作一个“元”，与其余4人共5个元作全排列答案7200种
八、不相邻问题“插空法”
对于某几个元素不相邻的排列问题，可先将其他元素排好，再将不相邻元素在已排好的元素之间及两端空隙中插入即可。
例7、在例6中， 若要求甲、乙、丙不相邻，则有多少种不同的排法？
先将4人排好，出现5个空，甲乙两人进5个空中的3个 答案1400

九。构造模型 “隔板法”
对于较复杂的排列问题，可通过设计另一情景，构造一个隔板模型来解决问题。

十一、分排问题“直排法”
把几个元素排成前后若干排的排列问题，若没有其它的特殊要求，可采取统一排成一排的方法来处理。
例10、7个人坐两排座位，第一排3个人，第二排坐4个人，则不同的坐法有多少种？
分析：7个人可以在前两排随意就坐，再无其它条件，故两排可看作一排来处理

近几年高考选择还出现一种题，列举，他用排列组合公式算不了，可是也算排列组合中的一种，这时你只能将可能一种一种列出了 2673希望对你有帮助！

---