【算法】(一)数组：Leetcode 7-实现整数的数字反转

【算法】(一)数组：Leetcode 7-实现整数的数字反转 题目描述

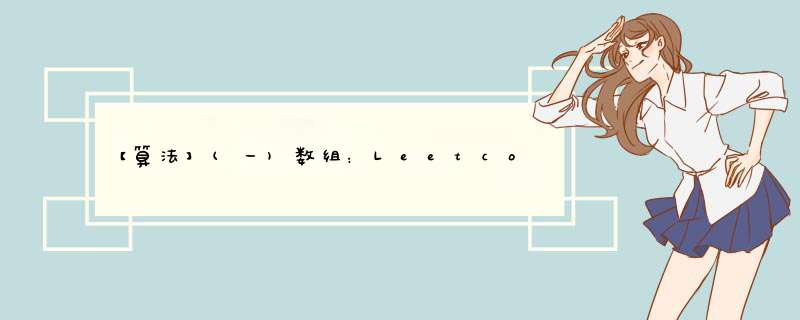
给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。如果反转后整数超过 32 位的有符号整数的范围 [−231,  231 − 1] ，就返回 0。假设环境不允许存储 64 位整数（有符号或无符号）。

​

解题思路 1C-comprehend：理解题意

理解题意关键点：分析问题根源，寻找可循方法，得到解题思路

解题思路：

       1.  逆序输出

        2. 首尾交换

2C-choose ：数据结构及算法思维选择

方案一：逆序输出（暴利解法）

        解题思路：先将整数转换成字符串，然后在转换成数组

 ❓ 字符串为什么要转换成数组？—— 字符串在Java语言中底层实现就是数组，低版本char，高版本byte

        数据结构：字符数组

        算法思维：遍历

方案二：收尾交换（优化解法）

        解题思路：先将整数转换成字符串，然后在转换成数组

        数据结构：字符数组

        算法思维：遍历

 数组介绍：

​

数组有三个特点：

        1. 容量固定不变，需在创建数组时指定

        2. 使用连续的物理空间存取数据

        3. 可以通过下标在O(1)的时间复杂度下读取数据

3C-code：基本解法及编码实现

解法一：暴利解法（逆序输出）

        解法步骤：

                1. 整数转成字符串，再转字符数组

                2. 反向遍历字符数组，并将元素存储到新数组中

                3. 将新数组转成字符串，再转成整数输出

        边界和细节问题：

                边界问题：

                        1. 数组索引越界

                        2. 数值溢出边界：溢出则返回0

                细节问题：

                        1. 首位不为0

                        2. 符号处理

        代码 (Java实现)：

       ✒️ 编码过程中先编写主体代码，调试通过后，再考虑边界和细节文艺

​

解法二：优化解法（收尾交换）

        解法步骤：

                1. 整数转成字符串，再转字符数组

                2. 交换首位(start)和末位(end)数字

                3. 循环 *** 作：依次交换第二(start++)和倒数第二个(end--)，直到数组剩下1个或0个元素。

                4. 将原数组转成字符串，再转成整数输出

        边界和细节问题：

                边界问题

                        1. 数组索引越界：数组长度为偶数，反转完成标志为start>end；为奇数时反转完成标志为start==end

                        2. 数值溢出边界：溢出则返回

                细节问题

                        1. 首位不为0

                        2. 符号处理

        代码：

​

4C-consider：思考更优解法

1. 剔除无效代码或优化空间消耗

         *** 作是必须的吗？

        数据结构是必须的吗？

2. 寻找更好的算法思维

        既然是整数，能否用数学思维？

        借鉴其它算法

5C-code：

最优解：数学思维解法

        解法步骤：

​

                1. 尝试拿个位数字

                        对10取模运算得到个位数字

                2. 让每一位数字变成个位数字

                        先除以10，再对10取模得到十位数字，循环上述 *** 作。

                3. 将每一位数字计算累加

                        将上次累加结果*10 + 新数字

        边界和细节问题：

                边界问题：

                        1. 从低位到高位处理，最高位结束

                                最高位 / 10 == 0

                                最高位 % 10 == 最高位

                        2. 数值溢出边界：溢出则返回0

                                用long类型存放，溢出int则返回0

                                新整数补充最后一位前判断溢出

        代码：

​

6C-change：

        题目变形：

                1. 如何解决对长整形数据进行反转？

                2. 如何解决对字符串进行反转？

        延伸扩展：

                在面对一些数字类题目时，思考是否可以利用数学特性来解决问题！

本节总结         6C解题法

                Comprehend： 理解题意

                Choose： 选择数据结构和算法思维

                Code： 基本解法编码

                Consider： 思考更优解

                Code： 最优解编码

                Change： 变形延伸

当我们在解决算法问题时，使用6C解题法，可以能够帮助我们快速理清楚思路，提高解决速度。

        数据结构：数组

                数组的特点：

                        1. 数组容量固定不变，需在创建数组时指定

                        2. 使用连续的物理空间在存取数据

                        3.可以通过下标在O(1)的时间复杂度下读取数据

        算法思维

                1. 遍历

                2. 逆序

                3. 原地交换

                5. 数学思维：取模、累加