【数据分析与挖掘实战】二手车价格预测1数据分析与特征构造详解(有数据集合代码)

【数据分析与挖掘实战】二手车价格预测1数据分析与特征构造详解(有数据集合代码) 一.题目概况

数据集：点击下载
根据给定的数据集，建立模型，二手汽车的交易价格。
来自 Ebay Kleinanzeigen 报废的二手车，数量超过 370,000，包含 20 列变量信息，为了保证 比赛的公平性，将会从中抽取 10 万条作为训练集，5 万条作为测试集 A，5 万条作为测试集 B。同时会对名称、车辆类型、变速箱、model、燃油类型、品牌、公里数、价格等信息进行 脱敏。

二.查看数据

import pandas as pd
import numpy as np

path = './data/'
## 1) 载入训练集和测试集；
Train_data = pd.read_csv(path+'train.csv', sep=' ')
Test_data = pd.read_csv(path+'testA.csv', sep=' ')
print('Train data shape:',Train_data.shape)
print('TestA data shape:',Test_data.shape)

Train_data.head()

# 三.分类/回归指标评价计算示例

## accuracy
import numpy as np
from sklearn.metrics import accuracy_score
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 1]
print('ACC:',accuracy_score(y_true, y_pred))

## Precision,Recall,F1-score
from sklearn import metrics
y_pred = [0, 1, 0, 0]
y_true = [0, 1, 0, 1]
print('Precision',metrics.precision_score(y_true, y_pred))
print('Recall',metrics.recall_score(y_true, y_pred))
print('F1-score:',metrics.f1_score(y_true, y_pred))

## AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))

# coding=utf-8
import numpy as np
from sklearn import metrics

# MAPE需要自己实现
def mape(y_true, y_pred):
    return np.mean(np.abs((y_pred - y_true) / y_true))

y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])

# MSE
print('MSE:',metrics.mean_squared_error(y_true, y_pred))
# RMSE
print('RMSE:',np.sqrt(metrics.mean_squared_error(y_true, y_pred)))
# MAE
print('MAE:',metrics.mean_absolute_error(y_true, y_pred))
# MAPE
print('MAPE:',mape(y_true, y_pred))

## R2-score
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
print('R2-score:',r2_score(y_true, y_pred))

四.数据分析 4.1载入各种数据科学以及可视化库:

• 数据科学库 pandas、numpy、scipy；
• 可视化库 matplotlib、seabon；
• 其他；

4.2载入数据：

• 载入训练集和测试集；
• 简略观察数据(head()+shape)；

#coding:utf-8
#导入warnings包，利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno

path = './data/'
## 1) 载入训练集和测试集；
Train_data = pd.read_csv(path+'train.csv', sep=' ')
Test_data = pd.read_csv(path+'testA.csv', sep=' ')

## 2) 简略观察数据(head()+shape)
Train_data.head().append(Train_data.tail())

Train_data.shape

4.3数据总览:

• 通过describe()来熟悉数据的相关统计量

## 1) 通过describe()来熟悉数据的相关统计量
Train_data.describe()

• 通过info()来熟悉数据类型

## 2) 通过info()来熟悉数据类型
Train_data.info()

4.4判断数据缺失和异常

• 异常值检测
• 查看每列的存在nan情况

## 1) 查看每列的存在nan情况
Train_data.isnull().sum()

# nan可视化
missing = Train_data.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()

通过以上两句可以很直观的了解哪些列存在 “nan”, 并可以把nan的个数打印，主要的目的在于 nan存在的个数是否真的很大，如果很小一般选择填充，如果使用lgb等树模型可以直接空缺，让树自己去优化，但如果nan存在的过多、可以考虑删掉

# 可视化看下缺省值
msno.matrix(Train_data.sample(250))

可以发现除了notRepairedDamage 为object类型其他都为数字 这里我们把他的几个不同的值都进行显示就知道了

Train_data['notRepairedDamage'].value_counts()

可以看出来‘ - ’也为空缺值，因为很多模型对nan有直接的处理，这里我们先不做处理，先替换成nan

Train_data['notRepairedDamage'].replace('-', np.nan, inplace=True)
Train_data['notRepairedDamage'].value_counts()
Test_data['notRepairedDamage'].value_counts()
Test_data['notRepairedDamage'].replace('-', np.nan, inplace=True)

del Train_data["seller"]
del Train_data["offerType"]
del Test_data["seller"]
del Test_data["offerType"]

4.5了解预测值的分布

• 总体分布概况（无界约翰逊分布等）

## 1) 总体分布概况（无界约翰逊分布等）
import scipy.stats as st
y = Train_data['price']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
plt.figure(3); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)

价格不服从正态分布，所以在进行回归之前，它必须进行转换。虽然对数变换做得很好，但最佳拟合是无界约翰逊分布

## 2) 查看skewness and kurtosis

```python
sns.distplot(Train_data['price']);
print("Skewness: %f" % Train_data['price'].skew())
print("Kurtosis: %f" % Train_data['price'].kurt())

``

Train_data.skew(), Train_data.kurt()

sns.distplot(Train_data.skew(),color='blue',axlabel ='Skewness')

sns.distplot(Train_data.kurt(),color='orange',axlabel ='Kurtness')

## 3) 查看预测值的具体频数
plt.hist(Train_data['price'], orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()

• 查看skewness and kurtosis
• 查看预测值的具体频数

查看频数, 大于20000得值极少，其实这里也可以把这些当作特殊得值（异常值）直接用填充或者删掉

# log变换 z之后的分布较均匀，可以进行log变换进行预测，这也是预测问题常用的trick
plt.hist(np.log(Train_data['price']), orientation = 'vertical',histtype = 'bar', color ='red') 
plt.show()

4.6特征分为类别特征和数字特征，并对类别特征查看unique分布

# 分离label即预测值
Y_train = Train_data['price']
# 这个区别方式适用于没有直接label coding的数据
# 这里不适用，需要人为根据实际含义来区分
# 数字特征
# numeric_features = Train_data.select_dtypes(include=[np.number])
# numeric_features.columns
# # 类型特征
# categorical_features = Train_data.select_dtypes(include=[np.object])
# categorical_features.columns


numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]

categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',]

# 特征nunique分布
for cat_fea in categorical_features:
    print(cat_fea + "的特征分布如下：")
    print("{}特征有个{}不同的值".format(cat_fea, Train_data[cat_fea].nunique()))
    print(Train_data[cat_fea].value_counts())

4.7数字特征分析

• 相关性分析

numeric_features.append('price')
## 1) 相关性分析
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending = False),'n')

f , ax = plt.subplots(figsize = (7, 7))

plt.title('Correlation of Numeric Features with Price',y=1,size=16)

sns.heatmap(correlation,square = True,  vmax=0.8)

del price_numeric['price']
## 2) 查看几个特征得 偏度和峰值
for col in numeric_features:
    print('{:15}'.format(col), 
          'Skewness: {:05.2f}'.format(Train_data[col].skew()) , 
          '   ' ,
          'Kurtosis: {:06.2f}'.format(Train_data[col].kurt())  
         )

## 3) 每个数字特征得分布可视化
f = pd.melt(Train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")

## 4) 数字特征相互之间的关系可视化
sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5',  'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()

Train_data.columns

• 查看几个特征得 偏度和峰值
• 每个数字特征得分布可视化
• 数字特征相互之间的关系可视化
• 多变量互相回归关系可视化

## 5) 多变量互相回归关系可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
# ['v_12', 'v_8' , 'v_0', 'power', 'v_5',  'v_2', 'v_6', 'v_1', 'v_14']
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)

v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)

v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)

power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)

v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)

v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)

v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)

v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)

v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)

v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)

4.8类型特征分析

• unique分布

## 1) unique分布
for fea in categorical_features:
    print(Train_data[fea].nunique())

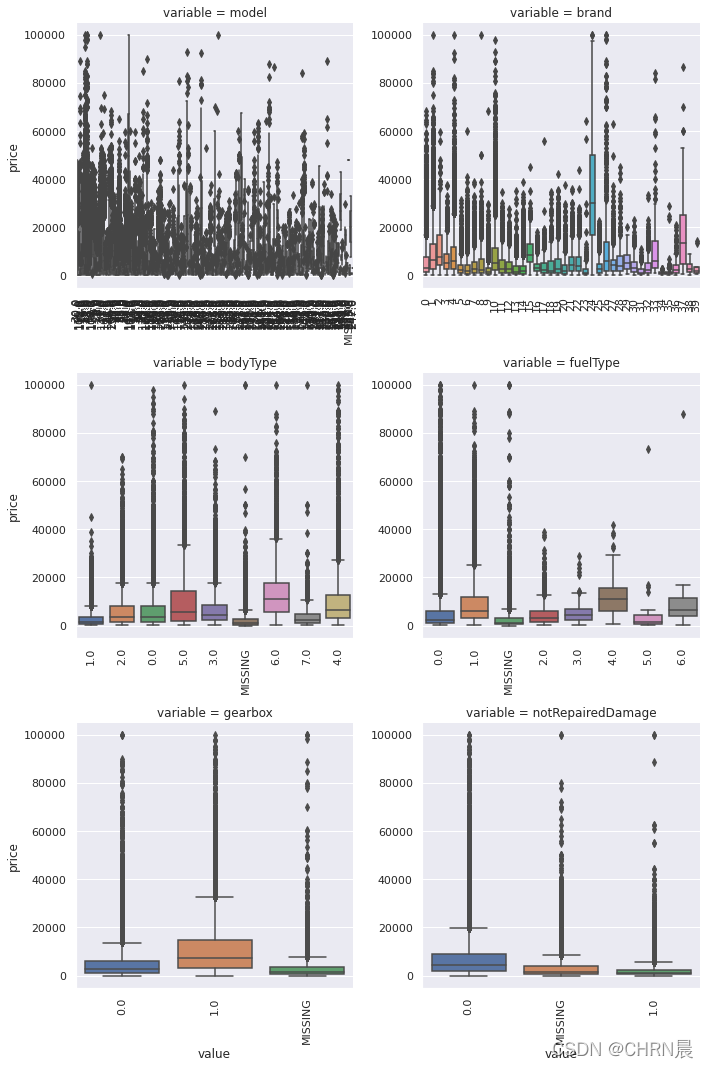
• 类别特征箱形图可视化

## 2) 类别特征箱形图可视化

# 因为 name和 regionCode的类别太稀疏了，这里我们把不稀疏的几类画一下
categorical_features = ['model',
 'brand',
 'bodyType',
 'fuelType',
 'gearbox',
 'notRepairedDamage']
for c in categorical_features:
    Train_data[c] = Train_data[c].astype('category')
    if Train_data[c].isnull().any():
        Train_data[c] = Train_data[c].cat.add_categories(['MISSING'])
        Train_data[c] = Train_data[c].fillna('MISSING')

def boxplot(x, y, **kwargs):
    sns.boxplot(x=x, y=y)
    x=plt.xticks(rotation=90)

f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(boxplot, "value", "price")
```![在这里插入图片描述](https://img-blog.csdnimg.cn/613e0e1eae2b41d79963058a9c6ac3d2.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ0hSTuaZqA==,size_20,color_FFFFFF,t_70,g_se,x_16)


 - 类别特征的小提琴图可视化

```python
## 3) 类别特征的小提琴图可视化
catg_list = categorical_features
target = 'price'
for catg in catg_list :
    sns.violinplot(x=catg, y=target, data=Train_data)
    plt.show()

• 类别特征的柱形图可视化类别

categorical_features = ['model',
 'brand',
 'bodyType',
 'fuelType',
 'gearbox',
 'notRepairedDamage']
 ## 4) 类别特征的柱形图可视化
def bar_plot(x, y, **kwargs):
    sns.barplot(x=x, y=y)
    x=plt.xticks(rotation=90)

f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(bar_plot, "value", "price")

• 特征的每个类别频数可视化(count_plot)

##  5) 类别特征的每个类别频数可视化(count_plot)
def count_plot(x,  **kwargs):
    sns.countplot(x=x)
    x=plt.xticks(rotation=90)

f = pd.melt(Train_data,  value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(count_plot, "value")

4.9用pandas_profiling生成数据报告

import pandas_profiling
pfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")

五.特征工程

常见的特征工程包括：

5.1异常处理：

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from operator import itemgetter

%matplotlib inline
path = './data/'
## 1) 载入训练集和测试集；
train = pd.read_csv(path+'train.csv', sep=' ')
test = pd.read_csv(path+'testA.csv', sep=' ')
print(train.shape)
print(test.shape)

5.1.1通过箱线图（或 3-Sigma）分析删除异常值；

# 这里我包装了一个异常值处理的代码，可以随便调用。
def outliers_proc(data, col_name, scale=3):
    """
    用于清洗异常值，默认用 box_plot（scale=3）进行清洗
    :param data: 接收 pandas 数据格式
    :param col_name: pandas 列名
    :param scale: 尺度
    :return:
    """

    def box_plot_outliers(data_ser, box_scale):
        """
        利用箱线图去除异常值
        :param data_ser: 接收 pandas.Series 数据格式
        :param box_scale: 箱线图尺度，
        :return:
        """
        iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
        val_low = data_ser.quantile(0.25) - iqr
        val_up = data_ser.quantile(0.75) + iqr
        rule_low = (data_ser < val_low)
        rule_up = (data_ser > val_up)
        return (rule_low, rule_up), (val_low, val_up)

    data_n = data.copy()
    data_series = data_n[col_name]
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
    print("Delete number is: {}".format(len(index)))
    data_n = data_n.drop(index)
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: {}".format(data_n.shape[0]))
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())
    
    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n
    
# 我们可以删掉一些异常数据，以 power 为例。  
# 这里删不删同学可以自行判断
# 但是要注意 test 的数据不能删 = = 不能掩耳盗铃是不是

train = outliers_proc(train, 'power', scale=3)

5.1.2BOX-COX 转换（处理有偏分布）； 5.1.3长尾截断； 5.2特征归一化/标准化： 5.2.1标准化（转换为标准正态分布）； 5.2.2归一化（抓换到 [0,1] 区间）； 5.2.3针对幂律分布，可以采用公式：log

# 训练集和测试集放在一起，方便构造特征
train['train']=1
test['train']=0
data = pd.concat([train, test], ignore_index=True, sort=False)
# 使用时间：data['creatDate'] - data['regDate']，反应汽车使用时间，一般来说价格与使用时间成反比
# 不过要注意，数据里有时间出错的格式，所以我们需要 errors='coerce'
data['used_time'] = (pd.to_datetime(data['creatDate'], format='%Y%m%d', errors='coerce') - 
                            pd.to_datetime(data['regDate'], format='%Y%m%d', errors='coerce')).dt.days

# 看一下空数据，有 15k 个样本的时间是有问题的，我们可以选择删除，也可以选择放着。
# 但是这里不建议删除，因为删除缺失数据占总样本量过大，7.5%
# 我们可以先放着，因为如果我们 XGBoost 之类的决策树，其本身就能处理缺失值，所以可以不用管；
data['used_time'].isnull().sum()

# 从邮编中提取城市信息，因为是德国的数据，所以参考德国的邮编，相当于加入了先验知识
data['city'] = data['regionCode'].apply(lambda x : str(x)[:-3])

# 计算某品牌的销售统计量，同学们还可以计算其他特征的统计量
# 这里要以 train 的数据计算统计量
train_gb = train.groupby("brand")
all_info = {}
for kind, kind_data in train_gb:
    info = {}
    kind_data = kind_data[kind_data['price'] > 0]
    info['brand_amount'] = len(kind_data)
    info['brand_price_max'] = kind_data.price.max()
    info['brand_price_median'] = kind_data.price.median()
    info['brand_price_min'] = kind_data.price.min()
    info['brand_price_sum'] = kind_data.price.sum()
    info['brand_price_std'] = kind_data.price.std()
    info['brand_price_average'] = round(kind_data.price.sum() / (len(kind_data) + 1), 2)
    all_info[kind] = info
brand_fe = pd.Dataframe(all_info).T.reset_index().rename(columns={"index": "brand"})
data = data.merge(brand_fe, how='left', on='brand')

5.3数据分桶：

# 数据分桶 以 power 为例
# 这时候我们的缺失值也进桶了，
# 为什么要做数据分桶呢，原因有很多，= =
# 1. 离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
# 2. 离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；
# 3. LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
# 4. 离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；
# 5. 特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化

# 当然还有很多原因，LightGBM 在改进 XGBoost 时就增加了数据分桶，增强了模型的泛化性

bin = [i*10 for i in range(31)]
data['power_bin'] = pd.cut(data['power'], bin, labels=False)
data[['power_bin', 'power']].head()

print(data.shape)
data.columns
print(data.shape)
data.columns

# 目前的数据其实已经可以给树模型使用了，所以我们导出一下
data.to_csv('data_for_tree.csv', index=0)
# 我们可以再构造一份特征给 LR NN 之类的模型用
# 之所以分开构造是因为，不同模型对数据集的要求不同
# 我们看下数据分布：
data['power'].plot.hist()

# 我们刚刚已经对 train 进行异常值处理了，但是现在还有这么奇怪的分布是因为 test 中的 power 异常值，
# 所以我们其实刚刚 train 中的 power 异常值不删为好，可以用长尾分布截断来代替
train['power'].plot.hist()

# 我们对其取 log，在做归一化
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
data['power'] = np.log(data['power'] + 1) 
data['power'] = ((data['power'] - np.min(data['power'])) / (np.max(data['power']) - np.min(data['power'])))
data['power'].plot.hist()

# km 的比较正常，应该是已经做过分桶了
data['kilometer'].plot.hist()

5.3.1等频分桶； 5.3.2分桶； 5.3.3Best-KS 分桶（类似利用基尼指数进行二分类）； 5.3.4卡方分桶； 5.4缺失值处理： 5.4.1不处理（针对类似 XGBoost 等树模型）； 5.4.2删除（缺失数据太多）； 5.4.3插值补全，包括均值/中位数/众数/建模预测/多重插补/压缩感知补全/矩阵补全等； 5.4.4分箱，缺失值一个箱； 5.5特征构造： 5.5.1构造统计量特征，报告计数、求和、比例、标准差等；

# 除此之外 还有我们刚刚构造的统计量特征：
# 'brand_amount', 'brand_price_average', 'brand_price_max',
# 'brand_price_median', 'brand_price_min', 'brand_price_std',
# 'brand_price_sum'
# 这里不再一一举例分析了，直接做变换，
def max_min(x):
    return (x - np.min(x)) / (np.max(x) - np.min(x))

data['brand_amount'] = ((data['brand_amount'] - np.min(data['brand_amount'])) / 
                        (np.max(data['brand_amount']) - np.min(data['brand_amount'])))
data['brand_price_average'] = ((data['brand_price_average'] - np.min(data['brand_price_average'])) / 
                               (np.max(data['brand_price_average']) - np.min(data['brand_price_average'])))
data['brand_price_max'] = ((data['brand_price_max'] - np.min(data['brand_price_max'])) / 
                           (np.max(data['brand_price_max']) - np.min(data['brand_price_max'])))
data['brand_price_median'] = ((data['brand_price_median'] - np.min(data['brand_price_median'])) /
                              (np.max(data['brand_price_median']) - np.min(data['brand_price_median'])))
data['brand_price_min'] = ((data['brand_price_min'] - np.min(data['brand_price_min'])) / 
                           (np.max(data['brand_price_min']) - np.min(data['brand_price_min'])))
data['brand_price_std'] = ((data['brand_price_std'] - np.min(data['brand_price_std'])) / 
                           (np.max(data['brand_price_std']) - np.min(data['brand_price_std'])))
data['brand_price_sum'] = ((data['brand_price_sum'] - np.min(data['brand_price_sum'])) / 
                           (np.max(data['brand_price_sum']) - np.min(data['brand_price_sum'])))
# 对类别特征进行 OneEncoder
data = pd.get_dummies(data, columns=['model', 'brand', 'bodyType', 'fuelType',
                                     'gearbox', 'notRepairedDamage', 'power_bin'])
print(data.shape)
data.columns

# 这份数据可以给 LR 用
data.to_csv('data_for_lr.csv', index=0)

5.5.2时间特征，包括相对时间和绝对时间，节假日，双休日等； 5.5.3地理信息，包括分箱，分布编码等方法； 5.5.4非线性变换，包括 log/ 平方/ 根号等； 5.5.5特征组合，特征交叉； 5.5.6仁者见仁，智者见智。 5.6特征筛选 5.6.1过滤式（filter）：

先对数据进行特征选择，然后在训练学习器，常见的方法有 Relief/方差选择发/相关系数法/卡方检验法/互信息法；

# 相关性分析
print(data['power'].corr(data['price'], method='spearman'))
print(data['kilometer'].corr(data['price'], method='spearman'))
print(data['brand_amount'].corr(data['price'], method='spearman'))
print(data['brand_price_average'].corr(data['price'], method='spearman'))
print(data['brand_price_max'].corr(data['price'], method='spearman'))
print(data['brand_price_median'].corr(data['price'], method='spearman'))

# 当然也可以直接看图
data_numeric = data[['power', 'kilometer', 'brand_amount', 'brand_price_average', 
                     'brand_price_max', 'brand_price_median']]
correlation = data_numeric.corr()

f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True,  vmax=0.8)

5.6.2包裹式（wrapper）：

直接把最终将要使用的学习器的性能作为特征子集的评价准则，常见方法有 LVM（Las Vegas Wrapper） ；

# k_feature 太大会很难跑，没服务器，所以提前 interrupt 了
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.linear_model import LinearRegression
sfs = SFS(LinearRegression(),
           k_features=10,
           forward=True,
           floating=False,
           scoring = 'r2',
           cv = 0)
x = data.drop(['price'], axis=1)
numerical_cols = x.select_dtypes(exclude = 'object').columns
x = x[numerical_cols]
x = x.fillna(0)
y = data['price'].fillna(0)
sfs.fit(x, y)
sfs.k_feature_names_ 

# 画出来，可以看到边际效益
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
import matplotlib.pyplot as plt
fig1 = plot_sfs(sfs.get_metric_dict(), kind='std_dev')
plt.grid()
plt.show()

5.6.3嵌入式（embedding）：

结合过滤式和包裹式，学习器训练过程中自动进行了特征选择，常见的有 lasso 回归；

5.7降维 5.7.1PCA/ LDA/ ICA； 5.7.2特征选择也是一种降维。