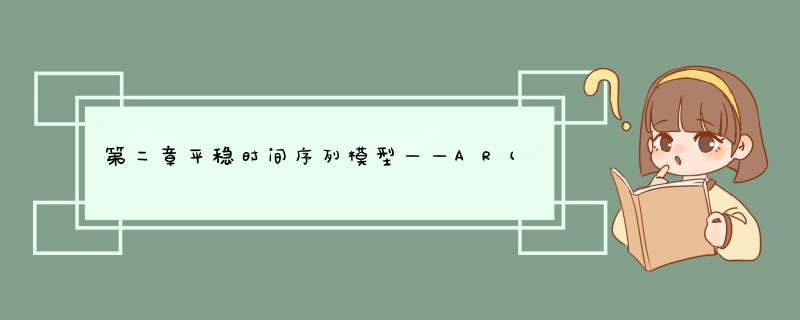
对于正态分布而言,不相关即可推出独立,所以如果该白噪声如果服从正态分布,则其还将互相独立。
2各种和模型
p阶移动平均过程:
q阶自回归过程:
自回归移动平均模型:
如果ARMA(p,q)模型的表达式的特征根至少有一个大于等于1,则{y(t)}为积分过程,此时该模型称为自回归秋季移动平均模型(ARIMA)
时间序列啊,不就是求个通项公式,然后求出一个非递推形式的表达式吗?
(这个公式和自变量t有关,然后以后只要知道t就能得到对应的y的预测值)
3弱平稳/协方差平稳:
均值和方差为常数(即同方差),协方差仅与时间间隔有关
4自相关系数:
5AR(1)模型(带白噪声的一阶差分方程)的平稳性:
(1)如果初始条件为y0:
则其解为
(我们通过其解来判断其是否平稳)
此时{y(t)}是不平稳的。
· 但是如果|a1|<1,其t足够大,则{y(t)}是平稳的。
均值:
方差:等于
协方差:等于
所以有结论:
(2)初始条件未知:
则其通解为:
{y(t)}平稳的条件为:
1 |a1|<1
2 且齐次解A(a1)^t为0:
序列从很久前开始(即t很大,且结合1,则为0),
或该过程始终平稳(A=0)
所以说,解的稳定性和序列的平稳性是不一样的。
这两条对所有的ARMA(p,q)模型都适用。
(对于任意的ARMA(p,q)模型,齐次解为0是平稳性必要条件) (ARMA(p,q)模型的齐次解为或) 6对于ARMA(2,1)模型的平稳性:
模型表达式为:(2.16)(截距项不影响平稳性,略去) 设其挑战解为:(用待定系数法)则系数应当满足方程:(2.17) 序列{阿尔法i}收敛的条件是方程(2.16)对于的齐次方程的特征根都在单位圆之内 (因为2.17中的差分方程对于的特征方程和方程2.16对于的特征方程是一模一样的) 我们之所以只考虑特解,是因为我们让齐次解为0. 此时该挑战解/特解:均值为: 方差为:(t很大时用级数求和) 协方差为:等于 所以其平稳性条件为(t很大): 1模型对应的齐次方程的特征方程的特征根在单位圆内 2齐次解为0。
7AR(p)模型的平稳性:
模型:
若其特征根都在单位圆之内,则其挑战解为:
{阿尔法i}这些待定系数会满足特征方程
(有木有发现其这个特征方程和模型对应的齐次方程的特征方程是一致的呢?)
该解的均值、方差、协方差为:
所以,所有特征根在单位圆内,则有
(早高阶差分方程平稳性的必要条件中提到),所以均值是有限长苏
所以AR(p)平稳条件为(t很大):
1模型对应的齐次方程的特征方程的特征根在单位圆内
2齐次解为0。
8MA(q)模型的平稳性:
模型为:
由于其级数求和为有限级数求和到q),所以MA(q)始终平稳
无限MA过程
模型为:
所以只要两个级数求和是有限的,就是MA(无穷)平稳的。
9ARMA(p,q)模型的平稳性:
模型为:(2.22)
其解的形式为:(2.23)
只要2.22的特征根都在单位圆内或者
逆特征方程的特征根在单位圆外,则(2.23)的每一项都平稳,所以其和也平稳,所以ARMA(p,q)模型平稳。
(书上没再给出更多解释了) 来自为知笔记(Wiz)
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)