C++——差值求和

C++——差值求和

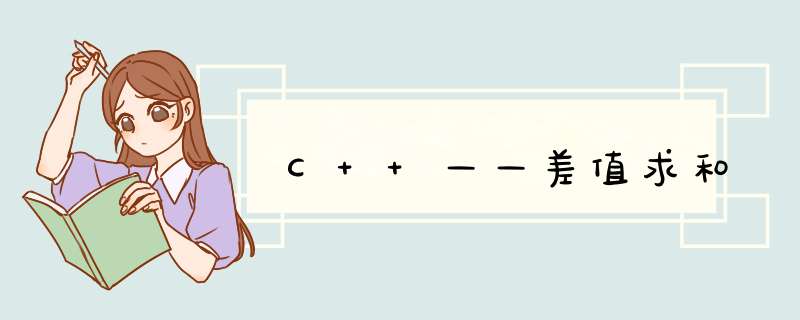
小明最近学习了差的绝对值，|a-b|表示a-b的绝对值，若a-b>=0，则|a-b|=a-b；若a-b<0，则|a-b|=-(a-b)。
经过几次练习，小明已经熟练掌握了差的绝对值，现在他找来了N个整数，开始任意取出两个数，求差的绝对值，再将所有差的绝对值相加。例如N=4，有4个整数，分别是1，2，3，4。任取两个数有6种取法，|1-2|=1，|1-3|=2，|1-4|=3，|2-3|=1，|2-4|=2，|3-4|=1，它们的和就是10。
由于运算量太大，累坏了小明。请你写一个程序帮他计算一下吧。

输入

第一行一个整数n，表示有n个整数
第二行n个整数，表示小明写下的n个整数

输出

输出一个数，表示任意两数差的绝对值之和。

样例输入 Copy

【样例1】
3
3 1 2
【样例2】
4
1 2 3 4

样例输出 Copy

【样例1】
4
【样例2】
10

提示

样例1解释：|3-1|=2,|3-2|=1,|1-2|=1，答案为4 

对于40%的数据，n<=1000,0<=每个数<=1000
对于70%的数据，输入数据保证第二行的n个数字从小到大有序。
对于100%的数据，n<=100000,0<=每个数<=1,000,000,000

提交状态

解题思路：采用差分

先将数组排序，举个例子， 比如1， 4， 5， 7 这四个数。很容易得出差分数组(带绝对值），即 b[1] = 2, b[2] = 1, b[3] = 2;

首先我们要明确如果我们要求1~7之间个元素绝对值差的和可以直接算， 但这题数据量庞大不支持此种算法，因此可以求1—4 + 1 —4 —5 + 1—4—5—7 的值， 而要求4—7就必须求4—5，通过4—5来推出4—7。

Code:

#include 
#include 
#include 
#include 
#include

using namespace std;

typedef long long LL;

const int N = 100010;

LL n, c, t, ans, s, f, j, h = 1, res;
LL a[N], b[N];

signed main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++ )  scanf("%d", &a[i]);
	sort(a + 1, a + n + 1);
	for(int i = 2; i <= n; i ++ )
	{
		b[++ j] = abs(a[i] - a[i - 1]);
	}
	for(int i = j; i >= 1; i -- )
	{
		ans += b[i] * h;
		res += ans;
		h ++;
	}
	cout << res << endl;
}