Ln1等多少

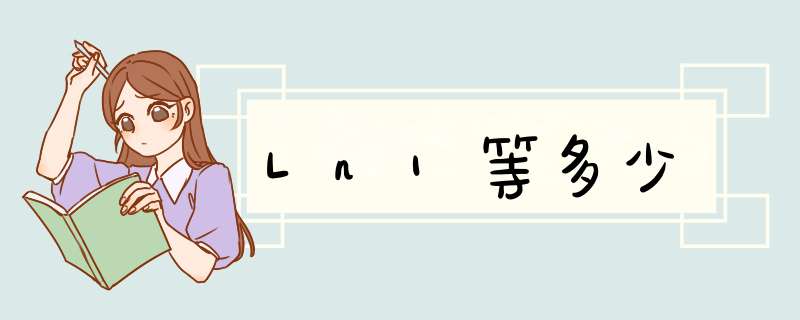
ln1等于0。

在物理学，生物学等自然科学中有重要的意义。一般表示方法为lnx。数学中也常见以logx表示自然对数。因为对数函数基本性质过定点（1，0） ，即x=1时，y=0，所以ln1等于0。

扩展资料

对数符号log出自拉丁文logarithm，最早由意大利数学家卡瓦列里（Cavalieri）所使用。20世纪初，形成了对数的现代表示。为了使用方便，人们逐渐把以10为底的常用对数及以无理数e为底的自然对数分别记作lgN和lnN。

如果a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作 x=logaN。其中，a叫做对数的底数，N叫做真数，x叫做“以a为底N的对数”。

参考资料来源：百度百科-对数

ln1=0。

计算过程：

ln1=loge（1），然后我们就可以利用反函数的思想来对式子进行求解，也就是让我们求e的几次方等于1。因为e^x>=0，又因为e^0=1，所以说得出结果为0。进而得出ln1=0。

自然对数是以常数e为底数的对数，记作lnN（N>0）。在物理学，生物学等自然科学中有重要的意义，一般表示方法为lnx。数学中也常见以logx表示自然对数。

扩展资料：

如果a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作x=loga N。其中，a叫做对数的底数，N叫做真数。

对数注意：

1、特别地，我们称以10为底的对数叫做常用对数（common logarithm），并记为lgN。

2、称以无理数e（e=2.71828…）为底的对数称为自然对数（natural logarithm），并记为lnN。

3、零没有对数。

4、在实数范围内，负数无对数。在虚数范围内，负数是有对数的。

对数在数学内外有许多应用。这些事件中的一些与尺度不变性的概念有关。例如， *** 的壳的每个室是下一个的大致副本，由常数因子缩放。这引起了对数螺旋。

参考资料来源：百度百科-对数

in1等于0。不管对数的底为多少，当N等于1的时候值都等于0，如果a的x次方等于N其中a大于0，且a不等于1，那么数x叫做以a为底N的对数logarithm，记作x等于logaN，其中a叫做对数的底数N叫做真数。

in1的特点

IN1表示为一个FB，FC的输入变量名如果是S7200的话，那么代表子程序的输入参数名LB0系统为这个输入参数分配了临时空间，数据长度为Byte地址为临时区的第0在数学中Ln1等于0可以利用方程转化的思想来求出答案，首先设Ln1等于X根据对数指数的转换可得出e^X等于1。

自然对数以常数e为底数的对数，记作lnN其中N大于0，一般表示方法为lnx，数学中也常见以logx表示自然对数，由于对数函数logx对于大的x而言增长非常缓慢，所以使用对数标度来压缩大规模科学数据，对数也出现在许多科学公式中，例如Tsiolkovsky火箭方程，Fenske方程或能斯特方程。