什么是模2运算啊

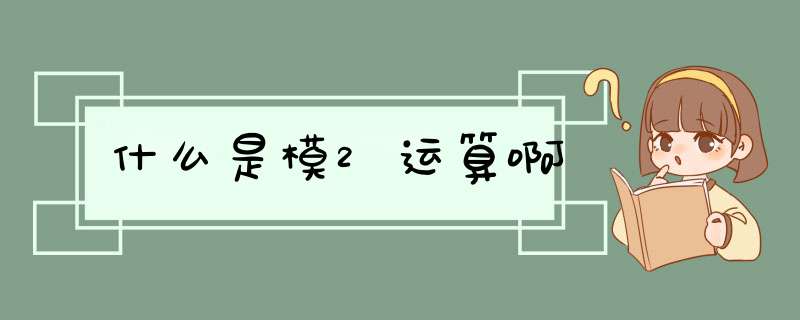
2，通俗的讲就是“除以2之后的

余数

”

比如3

mod

2

=

1

4

mod

2

=

0

可以看出，模2之后结果要么是0要么是1，{0,

1}就是2的

剩余类

。

模2加法运算定义为：

0＋0＝0        0＋1＝1        1＋0＝1        1＋1＝0

例如0101＋0011＝0110，列竖式计算：

0 1 0 1

＋0 0 1 1

──────

0 1 1 0

模2减法运算定义为：

0－0＝0        0－1＝1        1－0＝1        1－1＝0

例如0110－0011＝0101，列竖式计算：

0 1 1 0

－0 0 1 1

──────

0 1 0 1

模2乘法运算定义为：

0×0＝0        0×1＝0        1×0＝0        1×1＝1

多位二进制模2乘法类似于普通意义上的多位二进制乘法，不同之处在于后者累加中间结果（或称部分积）时采用带进位的加法，而模2乘法对中间结果的处理方式采用的是模2加法。

例如1011×101＝100111，列竖式计算：

1 0 1 1

×  1 0 1

──────

1 0 1 1

0 0 0 0

1 0 1 1

────────

1 0 0 1 1 1