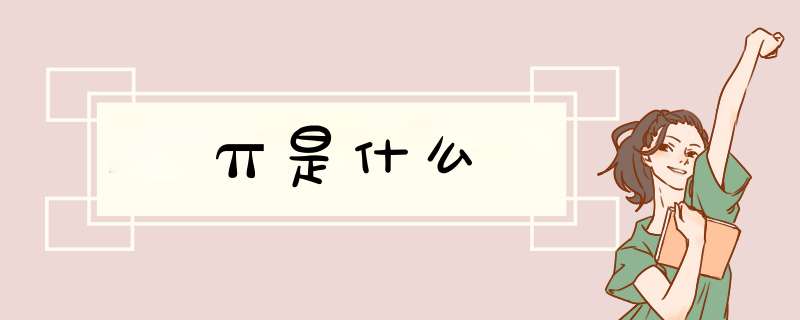
π是圆周率(Pi),圆的周长与直径的比值。一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
π是无限不循环小数,约等于3.141592654。
π也等于圆形之面积与半径平方之比。是精确计算圆周长、圆面积、球体积等几何形状的关键值。 在分析学里,π可以严格地定义为满足sin x = 0的最小正实数x。
扩展资料:
特性
把圆周率的数值算得这么精确,实际意义并不大。现代科技领域使用的圆周率值,有十几位已经足够了。如果以39位精度的圆周率值,来计算宇宙的大小,误差还不到一个原子的体积 [1] 。以前的人计算圆周率,是要探究圆周率是否循环小数。
自从1761年兰伯特证明了圆周率是无理数,1882年林德曼证明了圆周率是超越数后,圆周率的神秘面纱就被揭开了。
参考资料:百度百科—圆周率
π是圆周率(Pi),圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
π是无限不循环小数,约等于3.141592654。
π也等于圆形之面积与半径平方之比,是精确计算圆周长、圆面积、球体积等几何形状的关键值,在分析学里,π可以严格地定义为满足sin x = 0的最小正实数x。
圆周率的具体介绍:
圆周率用希腊字母π(读作[paɪ])表示,是一个常数(约等于3.141592654),是代表圆周长和直径的比值。它是一个无理数,即无限不循环小数。
1665年,英国数学家约翰·沃利斯(John Wallis)出版了一本数学专著,其中他推导出一个公式,发现圆周率等于无穷个分数相乘的积。2015年,罗切斯特大学的科学家们在氢原子能级的量子力学计算中发现了圆周率相同的公式。
2019年3月14日,谷歌宣布圆周率现已到小数点后31.4万亿位。
2021年8月17日,美国趣味科学网站报道,瑞士研究人员使用一台超级计算机,历时108天,将著名数学常数圆周率π计算到小数点后62.8万亿位,创下该常数迄今最精确值记录。
π,现在的输入法一般都支持输入“π”这个字符,只需要你打出“pai”这个拼音,就能在备选栏中找到“π”。
什么是“π”?
圆周率是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比,是精确计算圆周长、圆面积、球体积等几何形状的关键值。在分析学里,π可以严格地定义为满足sinx=0的最小正实数x。
中国古代关于圆周率的计算:
中国古算书《周髀算经》(约公元前2世纪)的中有“径一而周三”的记载,意即取π=3。汉朝时,张衡得出π²/16≈5/8,即π≈√10(约为3.162)。这个值虽然不太准确,但它简单易理解。
公元263年,中国数学家刘徽用“割圆术”计算圆周率,他先从圆内接正六边形,逐次分割一直算到圆内接正192边形。他说:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,最终他求得π≈3.1416。
公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927。在之后的800年里,祖冲之计算出的π值都是最准确的。
参考资料来源:百度百科-圆周率
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)