matlab中“SVD”和“EIG”的区别是什么

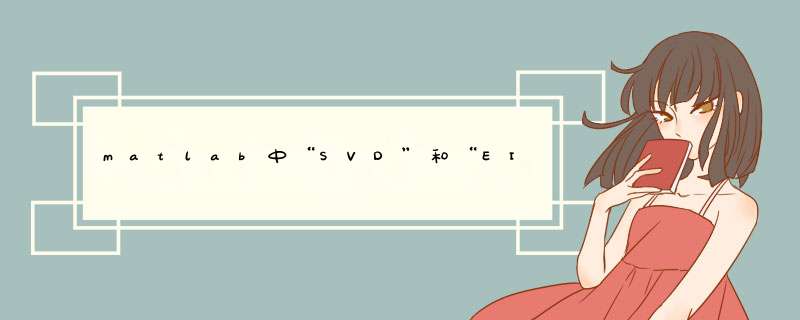
svd得到的是A的奇异值，eig得到的是A的特征值。A'表示A的转置矩阵，A'A的n个非负特征值的平方根叫作矩阵A的奇异值。记为σi(A)。

（1）S=svd（A）表示对矩阵A进行SVD分解，分解的结果是得到3个矩阵，如果返回值只有一个，那么可以得到A的奇异值向量。

（2）eig（A）表示求矩阵A的特征值。

MATLAB 是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

MATLAB是matrix和laboratory两个词的组合，意为矩阵工厂(矩阵实验室)。是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式，代表了当今国际科学计算软件的先进水平。

假定拟计算一般矩阵A的Moore-Penrose广义逆A+,

1)对A做SVD:

A = U S V, 其中 U, V为酉方阵, S为一般对角阵;

2)将S非零元取逆, 零元不变, 然后专置得到一个一般对角阵T;

3)则广义逆为A+ = V T U, 其中 表示取矩阵的复共轭

请采纳。

打开一个终端，执行下面的命令：sudo rm /var/crash/

这个 *** 作会删除所有在/var/crash目录下的所有内容。这样你就不会再被这些报告以前程序错误的d窗所扰。但是如果又有一个程序崩溃了，你就会再次看到“检测到系统程序错误”的错误。你可以再次删除这些报告文件，或者你可以禁用Apport来彻底地摆脱这个错误d窗。

2、彻底地摆脱Ubuntu中的系统错误d窗

要禁止Apport，并且彻底地摆脱Ubuntu系统中的程序崩溃报告，打开一个终端，输入以下命令：

gksu gedit /etc/default/apport

这个文件的内容是：

# 设置0表示禁用Apportw，或者1开启它。

# 你可以用下面的命令暂时关闭它：

# sudo service apport start force_start=1

enabled=1

把enabled=1改为enabled=0。保存并关闭文件。完成之后你就再也不会看到d窗报告错误了。很显然，如果我们想重新开启错误报告功能，只要再打开这个文件，把enabled设置为1就可以了。

旅行商问题

奇异值分解(SVD)的原理详解及推导



处女座程序员的朋友

原创

关注

2点赞·6156人阅读

1 写在前面

最近整理推荐系统模型的时候， 第二个模型打算整理一下隐语义模型， 这里面绕不开一种思想就是矩阵分解， 而作为矩阵分解的经典方法SVD感觉这次有必要学学了， SVD不仅是一个数学问题，在工程应用中的很多地方都有它的身影，比如我之前在白话机器学习篇说到了PCA， 那是一种经典的降维方式， 而SVD同样的也可以用于降维， 并且掌握了SVD原理后再去看PCA那是相当简单的，在推荐系统方面，SVD更是名声大噪，在2006年， Koren将它应用于推荐系统并获得了Netflix大奖， 因此在推荐系统中也就出来了隐语义模型(Latent Factor Model)或者叫矩阵分解模型(Matrix Fatcorization)， 它们的核心思想是通过寻找隐含特征来联系用户兴趣和商品，说白了其实就是把协同过滤里面的共现矩阵分解成了两个矩阵相乘的方式。 这个在具体整理的时候再谈， 总之， 这里面绕不开的一个名词就是SVD， 尽管数学上的这种SVD矩阵分解由于它对矩阵稠密的要求和计算复杂度大不太直接用于协同过滤里面的共现矩阵，但是源思想没变， 所以在这里先整理一下SVD的原理， 防止在整理矩阵分解模型的时候遇到SVD， RSVD， ASVD， SVD++等各种名词的时候一脸懵逼哈哈。

定理和推论

定理：设A为mn阶复矩阵，则存在m阶酉阵U和n阶酉阵V，使得：

A = USV’

其中S=diag(σi,σ2,……,σr)，σi>0 (i=1,…,r)，r=rank(A)。

推论：

设A为mn阶实矩阵，则存在m阶正交阵U和n阶正交阵V，使得

A = USV’

其中S=diag(σi,σ2,……,σr)，σi>0 (i=1,…,r)，r=rank(A)。

说明：

1、 奇异值分解非常有用，对于矩阵A(mn)，存在U(mm)，V(nn)，S(mn)，满足A = USV’。U和V中分别是A的奇异向量，而S是A的奇异值。AA'的正交单位特征向量组成U，特征值组成S'S，A'A的正交单位特征向量组成V，特征值（与AA'相同）组成SS'。因此，奇异值分解和特征值问题紧密联系。

2、奇异值分解提供了一些关于A的信息，例如非零奇异值的数目（S的阶数）和A的秩相同，一旦秩r确定，那么U的前r列构成了A的列向量空间的正交基。

正交矩阵

正交矩阵是实数特殊化的酉矩阵，因此总是正规矩阵。尽管我们在这里只考虑实数矩阵，

这个定义可用于其元素来自任何域的矩阵。正交矩阵毕竟是从内积自然引出的，对于复

数的矩阵这导致了归一要求。注意正交矩阵的定义：n阶‘实矩阵’ A称为正交矩阵，如果：A×A′=E（E为单位矩阵，

A'表示“矩阵A的转置矩阵”。） 若A为正交阵，则下列诸条件是等价的:

1) A 是正交矩阵

2) A×A′=E（E为单位矩阵）

3) A′是正交矩阵

4) A的各行是单位向量且两两正交

5) A的各列是单位向量且两两正交

6) (Ax,Ay)=(x,y) x,y∈R

方法

1搜送［visio viewer］，找到微软的官方下载地址。

2然后按照提示下载并安装软件即可。

3如果说需要编辑 vsd格式的文件，那么需要下载专门的软件才行，如Microsoft Visio 2010。

注意事项

安装完成，双击svd文件就能打开。

以上就是关于matlab中“SVD”和“EIG”的区别是什么全部的内容，包括:matlab中“SVD”和“EIG”的区别是什么、matlab中SVD分解函数的问题、ubuntu系统启动时reservedsvdcode108等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！