
最简单的神经网络,仅由一个“神经元”构成,所谓神经网络就是将许多个单一“神经元”联结在一起,这样,一个“神经元”的输出就可以是另一个“神经元”的输入。
文章描述采用反向传播算法训练多层神经网络的学习过程。为了说明这个过程,使用了具有两个输入和一个输出的三层神经网络,如下图所示:
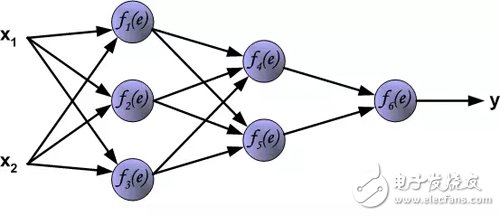
每个神经元由两部分组成。第一部分是输入信号和权重系数的加权和。第二部分是非线性函数,称为神经元激活函数。信号e是加权和的输出(加法器的输出)信号。y=f(e)是非线性函数(元件)的输出信号。信号y也是神经元的输出信号。
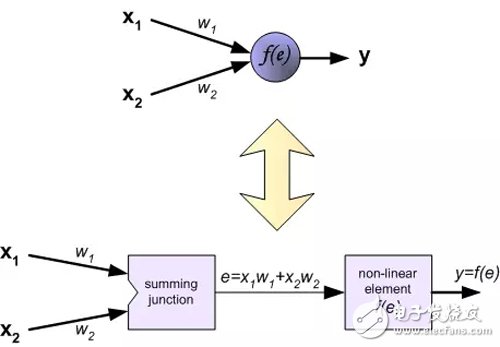
要训练神经网络,我们需要“训练数据集”。训练数据集是由对应目标z(期望输出)的输入信号(x_1和 x_2)组成。神经网络的训练是一个迭代过程。在每个迭代中,使用来自训练数据集的新数据修改网络节点的加权系数。整个迭代由前向计算和反向传播两个过程组成。
前向计算:每个学习步骤从来自训练集的两个输入信号开始。前向计算完成之后,我们可以确定每层网络中每个神经元的输出信号值(译者注:隐藏层神经元的误差是没有的,因为训练数据集中没有隐藏层的目标值)。下图显示了信号如何通过网络传播,符号w(xm) 表示网络输入x_m和神经元n之间的连接权重。符号y_n 表示神经元n的输出信号。
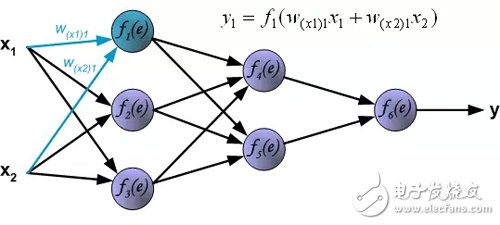
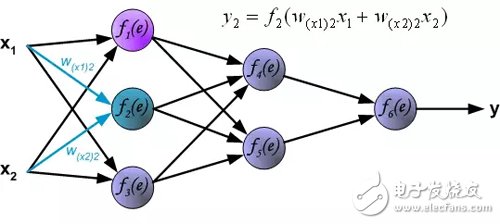
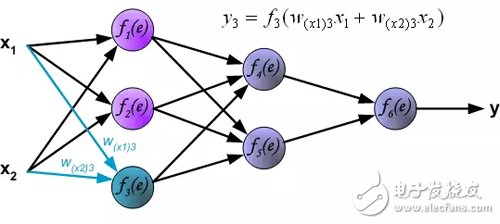
隐藏层信号传播。符号w_mn表示神经元m的输出和后一层神经元n的输入之间的连接权重 。
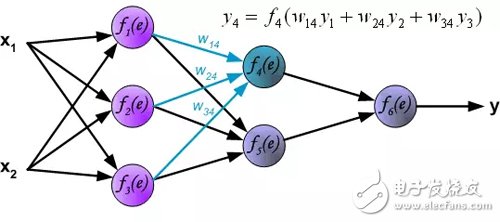

输出层信号传播:
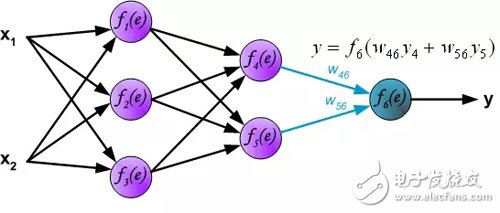
在下一个算法步骤中,将网络y的输出信号与训练数据集中的输出值(目标)进行比较。差异称为输出层神经元的误差信号δ。
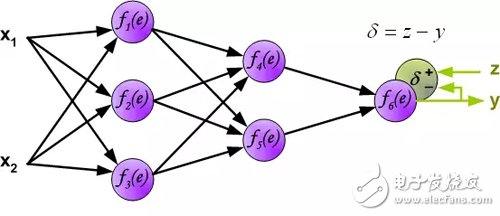
因为隐层神经元的输出值(训练集没有隐藏层的目标值)是未知的,所以不可能直接计算内部神经元的误差信号。多年来,一直没有找到训练多层神经网络的有效方法。直到在八十年代中期,反向传播算法才被制定出来。反向传播算法是将误差信号δ(在单个训练步骤中计算)传播回所有神经元,对于神经元来说,误差信号反向传播。
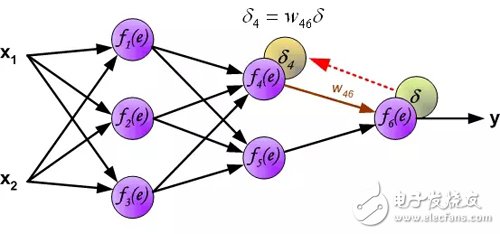
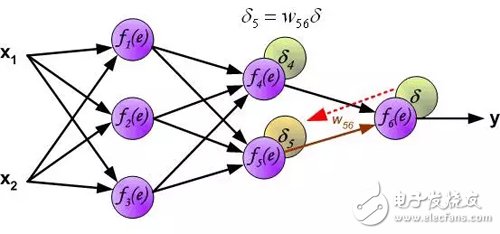
用于传播误差的权重系数w_mn等于前向计算使用的权重系数,只是数据流的方向改变(信号从输出到输入一个接一个地传播)。该技术用于所有网络层。如果误差是来自多个神经元,则把它们加起来(译者注:反向来看,也是加权和)。下图所示:
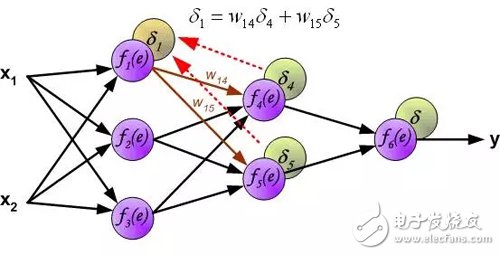
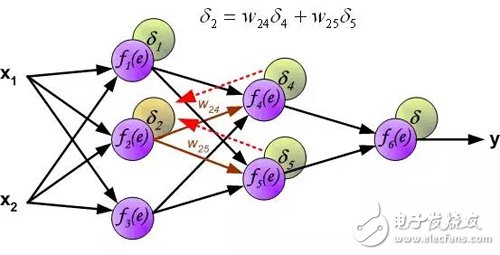
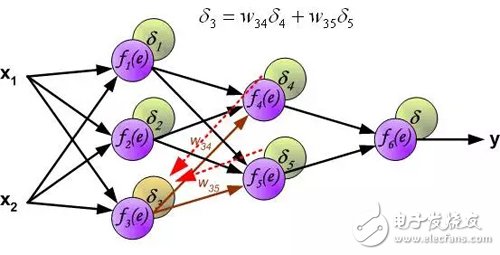
计算每个神经元的误差信号,用于修改每个神经元输入连接的加权系数。在下面的公式中, df(e)/de表示神经元激活函数的导数。影响权重的因素除了神经元激活函数的导数之外,还有反向传播的误差信号,以及神经元输入方向连接的前一个神经元。(译者注:这里忽略了推导过程,直接给出权重的修改方法。具体的推导过程参考我的前一篇文章:《误差反向传播算法浅解》。原理是一样的,影响权重的三个因素体现在下面的公式中。)。
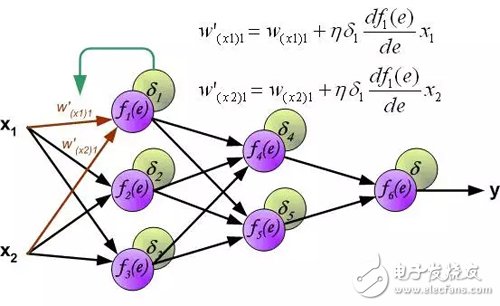
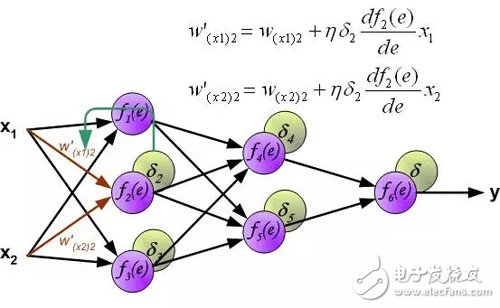
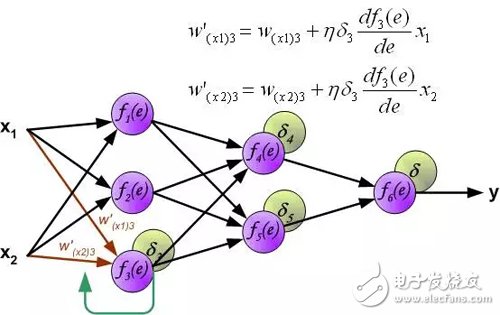
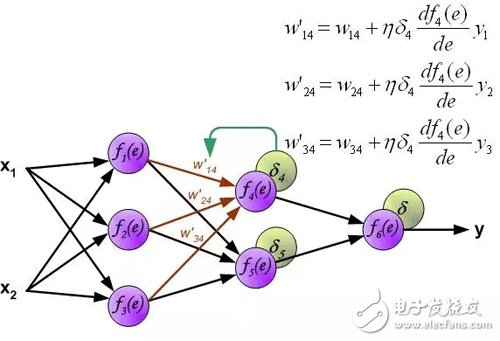
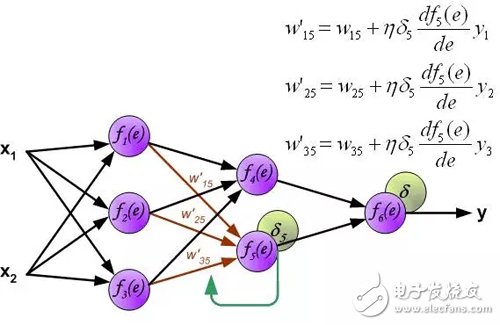
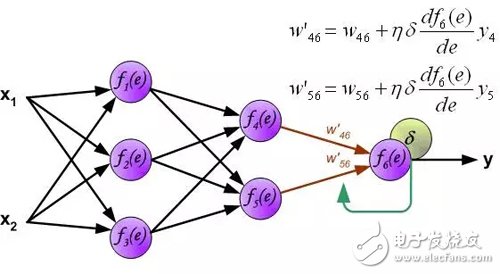
其中系数η影响网络训练速度。有几种技术来选择此参数。第一种方法是开始具有较大参数值。当权重系数正在建立时,参数逐渐减少。第二个方法是开始用小参数值进行训练。在训练过程中,参数逐渐增加,然后在最后阶段再次下降。开始具有低参数值的训练过程能够确定权重系数。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)