交流净化电源中等效电感的分析

交流净化电源中等效电感的分析

摘要：在设计新型交流净化电源时，研究等效电感L和晶闸管触发角θ之间的关系很有必要。本文探讨了它们之间的关系，推导出它们之间的关系式。

关键词：双向晶闸管等效电感

Analysis of the Equivalent Inductance of the Clean AC Power Supply

Abstract: As a new clean AC power supply is designed,it is very necessary that know the relaTIonship between the equivalent inductance “ L” and the triac turn－ on angle “ θ ” . In this paper,the relaTIonship between them is analyzed,a calculaTIon formular between them is derived.

Keywords: Triac, Equivalent inductance

1引言

目前，在各种交流稳压电源中，采用正弦能量分配技术的交流净化电源是一种新型的技术先进的稳压电源。其典型的实用电路简图如图1所示。

实际上，这种电路主要是通过改变晶闸管的触发角θ，来改变A、B间的等效电感量，从而起到稳定输出电压的作用。

在实际设计、制造过程中，如果知道A、B间的等效电感随触发角θ的变化情况，对设计出稳定可靠的电源是很有帮助的。为此，有必要分析一下A、B间的等效电感量是如何随触发角θ变化的。

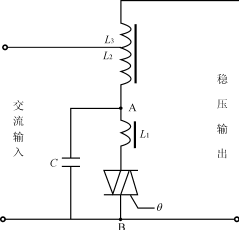
图1交流净化电源典型实用电路

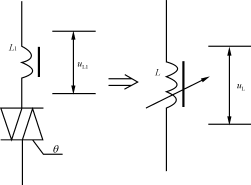
图2等效电路示意图

2等效电感的分析

将由电感L1和晶闸管构成的串联电路等效为可变电感L，如图2所示。

设加在L1两端的交流电压为

uL=Umsinβ

则电感L1上的电压波形uL1如图3中实线所示。图中θ为触发角，在0～π之间变化。当θ=0时，晶闸管完全导通；当θ=π时，晶闸管完全截止。

uL1的表达式为，　　现将uL1按傅立叶级数展开(ancosnβ＋bnsinnβ)(1)

上式中=0(n=0,1,2,…)

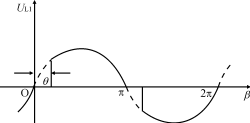
图3电感L1上的电压波形

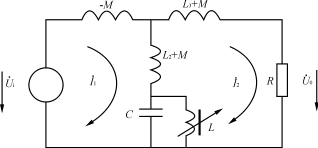
图4交流净化电源去耦等效电路

故式（1）可表示为（2）

上式中

(n=3,5,7,…)n=1时，(3)

在实际设计交流净化电源时，由于对3次和5次谐波都加有滤波电路，而7次以上的谐波分量很小，所以在实际计算中，可以近似地将3次以上的谐波分量略去不计。故可近似认为

uL1≈b1sinβ

又，由于IL1=IL，因此即则(4)

式（4）即为表征等效电感L与晶闸管触发角θ之间关系的近似计算公式。

　　（编者注：此式与本刊总第11期有关文章中的推导结果不完全一致，设定的条件也不相同。）

3等效电感的实际应用

知道了等效电感的近似计算公式，在实际设计交流净化电源时，可将图1等效为如图4所示的去耦等效电路，使复杂的问题简单化。

用网络分析法，可得如下方程(5)(6)其中

　　而L与L1之间的关系由式（4）得出。

　　在负载为纯阻性的情况下，有　　将以上关系式代入式（5）、（6）可以求得，(7)

由上式可知，要使输出电压保持稳定，在参数L1、L2、L3、C及负载R确定的情况下，当输入交流电压发生变化时，则Lx（实际上表现为晶闸管触发角θ）亦相应要发生变化。

在实际设计时，根据式（4）和式（7）选择合适的晶闸管触发角θ及参数L1、L2、L3、C，有助于设计出不同功率、不同稳压范围的交流净化电源，并使设计更加合理，更加稳定可靠。

4实验结果分析

下面来验证式（4）的可行性

现对一实用的3kVA交流净化电源进行分析。该电源的主要参数为：

L1=60mH，L2=193mH，L3=21.4mH，C=20μF，R=16.1Ω，Uo=220V。

根据式（4）和式（7）可算出，Ui与θ之间的理论计算值如表1中上格所示。

利用同步示波器和调压器，实测出Ui与θ之间的数据如表1中下格所示。

表1VI与θ的理论与实测值

　 198V 220V 253V 理论计算值 104° 122° 137° 实测值 105° 124° 139°

VI由表1可知，θ的理论计算值与实测值基本吻合，故等效电感L的计算公式（4）经实验证明是行之有效的。

5结语

运用傅立叶级数，并结合实际情况，推导出了交流净化电源中等效电感L和晶闸管触发角θ之间的关系式，并通过实验进行了验证。利用这个关系式，有助于设计出不同规格的交流净化电源，并使设计更为合理可靠。

参考文献

1郑君里.信号与系统.北京:人民邮电出版社，1982