
最近在做基于MIPS指令集的单周期CPU设计,其中的ALU模块需要用到加法器,但我们知道普通的加法器是串行执行的,也就是高位的运算要依赖低位的进位,所以当输入数据的位数较多时,会造成很大的延迟,影响整个CPU的性能,为了减小这种延迟,遂采用超前进位加法器(也叫先行进位加法器),下面来介绍一下设计的原理:
设二进制加法器第 i 位为Ai, Bi,输出为Si,进位输入为Ci,进位输出为C(i+1),则有:
Si = Ai ⊕ Bi ⊕ Ci (1-1)
C(i + 1) = Ai * Bi + Ai * Ci + Bi * Ci = Ai * Bi +(Ai+Bi)* Ci (1-2)
令Gi = Ai * Bi , Pi = Ai + Bi,则: C(i + 1) = Gi + Pi * Ci
当 Ai 和 Bi 都为1时,Gi = 1, 产生进位C(i+1) = 1;
当 Ai 和 Bi 有一个为1时,Pi = 1,传递进位C(i+1)= Ci;
(说明:“*”表示与逻辑、“+”表示或逻辑、“⊕”表示异或逻辑)
因此Gi定义为进位产生信号,Pi定义为进位传递信号。Gi的优先级比Pi高,也就是说:当Gi = 1时(当然此时也有 Pi = 1),无条件产生进位,而不管Ci是多少;当Gi = 0 而 Pi = 1时,进位输出为Ci,跟Ci之前的逻辑有关.
第一步:设计4位超前进位加法器 (至于为什么要先设计4位的,后面有详解)
举例:设4位加数和被加数为 A 和 B,进位输入为C_in,进位输出为C_out,对于第 i 位的进位产生Gi = Ai * Bi ,进位传递Pi = Ai + Bi , i = 0,1,2,3 。于是各级进位输出,递归的展开Ci,有:
C0 = C_in
C1 = G0 + P0*C0
C2 = G1 + P1*C1 = G1 + P1*G0 + P1*P0 *C0
C3 = G2 + P2*C2 = G2 + P2*G1 + P2*P1*G0 + P2*P1*P0*C0
C4 = G3 + P3*C3 = G3 + P3*G2 + P3*P2*G1 + P3*P2*P1*G0 + P3*P2*P1*P0*C0 (1-3)
C_out = C4
由此可以看出,各级的进位彼此独立,只与输入数据 Ai、Bi 和 C_in有关,而且并行产生,不就达到了设计目的——将各级间的进位级联传播给去掉了,减小了串行进位产生的延迟。
实现上述逻辑表达式(1-3)的电路称为超前进位部件(Carry Lookahead Unit),也称为CLA部件。通过这种进位方式实现的加法器称为超前进位加法器。因为各个进位是并行产生的,所以是一种并行进位加法器。
4位CLA部件电路如图1所示:
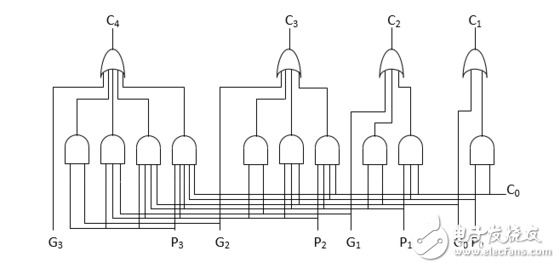
图1:4位CLA超前部件电路
(可能有人就想到,如果要设计32位超前进位加法器,是不是可以按照同样的方法直接推导到C32,就可以一次性并行产生所有位的进位。。。但是,我们想想,根据表达式,进位越往后,比如C5、C6......C31、C32,表达式会越来越复杂,这是因为增加了逻辑门的输入端个数,将会使得电路中需要具有大驱动信号和大扇入门,这会大大增加门的延迟,起不到提高电路性能的作用,这种方法叫做全先行进位,而当位数较多时,很显然这种方式并不现实,因此更多位数的加法器可通过4位CLA部件和4位超前进位加法器来实现,后面再细说)
* 4位超前部件完成了,现在来完成4位超前进位加法器:
首先每一位都会产生进位传递信号和进位产生信号,然后将四位数据分别产生的进位传递信号和进位产生信号送到4位CLA部件,供CLA并行产生每一位的进位信号Ci,然后再送回给每一位的低进位(C_in),就完成了4位超前进位加法器,听不懂,没关系,看下图:
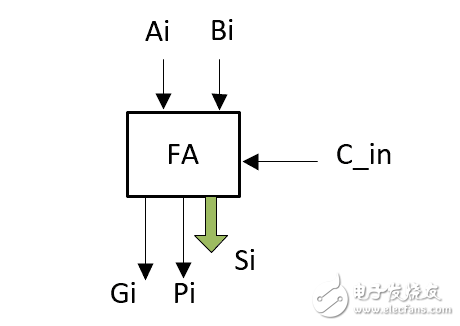
图2:1位加法器
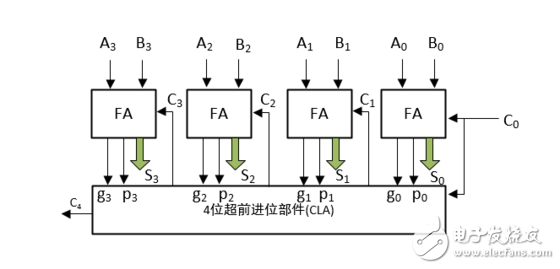
图3:4位超前进位加法器
说明:1位加法器如图2所示,输入有A、B两个加数,还有来自低位的进位C_in,输出有得到的和 Si ,还有 进位产生信号Gi和进位传递信号Pi,之所以引出这两个信号,是为了为后面的4位超前进位加法器做铺垫,有人可能奇怪为什么没有向高位的进位位,这是因为每一位的进位位是由CLA部件产生的,我们用四个如图2所示的1位加法器和一个如图1所示的4位超前进位部件,就组成了图3所示的4位超前进位加法器,至此我们也就完成了4位超前进位加法器的设计。
那么,问题来了,4位超前进位加法器和我们最初要设计的32位超前进位加法器有什么联系呢?有经验的朋友很快就能反应过来,是不是可以用八组4位超前进位加法器级联起来,完成32位的设计,但是,如果仅仅按照普通的级联,也就是将八组4位超前进位加法器串联起来,整个设计相当于组内超前进位,组间串行进位,这种方法是可行的,但不是我们的目的,因为它还是会影响整个系统的性能,为了达到最优的设计方法,我们采用组内超前进位,组间也是超前进位的方法进行设计,这种方法叫做两级或多级先行进位加法器。
问题又来了,采用组内和组间都是超前进位的方式,到底该怎么设计呢?其实我们可以类比4位加法器的设计,为了完成4位的超前进位加法器,我们把1位加法器引出了它的进位产生信号Gi和进位传递信号Pi,供4位CLA使用,那么我们是否可以把4位超前进位加法器的进位产生信号Gm和进位传递信号Pm也引出来,然后用四组4位超前进位加法器和一个4位CLA完成16位超前进位加法器的设计呢,答案当然是可以的。
首先,我们对图3所示的4位超前进位加法器进行封装,并且引出进位产生信号Gm和进位传递信号Pm,如图4所示:
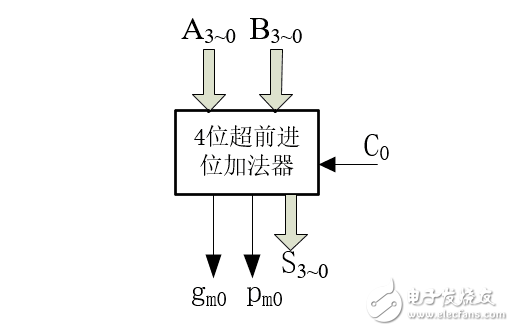
图4:封装后的4位超前进位加法器
说明:图4也是4位超前进位加法器,它和图3的区别是引出了进位产生信号Gm和进位传递信号Pm,有心的朋友会发现它和图2所示的1位加法器很相似,不同的地方仅仅是位数变成了四位,既然和1位加法器相似,那么我们就可以按照同样的方法用四个图4所示的4位超前进位加法器和一个CLA设计16位超前进位加法器,问题又来了,图4所示的4位超前加法器的进位产生信号Gm和进位传递信号Pm怎么来的呢?
首先来看1位加法器的进位产生信号Gi和进位传递信号Pi是怎么来的:
既然是1位加法器,那么它的进位信号是C1,
由 C(i + 1) = Ai * Bi + Ai * Ci + Bi * Ci = Ai * Bi +(Ai+Bi)* Ci 得:
当 i = 0 时,即1位加法器的进位信号 C1 = A0 * B0 + (A0 + B0)* C0
我们把 (A0 * B0)叫做进位产生信号Gi,把(A0 + B0)叫做进位传递信号Pi 【原因前面已经讲过】
显然 Gi 和 Pi 分别时1位加法器的进位产生信号和进位传递信号.
再来看4位加法器的进位产生信号Gm和进位传递信号Pm该怎么来:
既然是4位加法器,那么它的进位信号是C4,
由 C(i + 1) = Ai * Bi + Ai * Ci + Bi * Ci = Ai * Bi +(Ai+Bi)* Ci 得:
当 i = 3 时,即4位加法器的进位信号
C4 = A3 * B3 + (A3 + B3)* C3
= G3 + P3*C3
= G3 + P3*G2 + P3*P2*G1 + P3*P2*P1*G0 +P3*P2*P1*P0*C0【在设计4位CLA时已经给出】
类比法得:把(G3 + P3*G2 + P3*P2*G1 + P3*P2*P1*G0)叫做进位产生信号Gm,(P3*P2*P1*P0) 叫做进位传递信号Pm,显然 Gm 和 Pm 分别是四位加法器的进位产生信号和进位传递信号.
第二步:设计16位超前进位加法器
首先每一个封装后的4位超前进位加法器都会都会输出进位产生信号和进位传递信号,将四个4位超前进位加法器输出的进位产生信号和进位传递信号输入到4位CLA中,供CLA产生每一个4位超前进位加法的低进位信号,如下图所示:
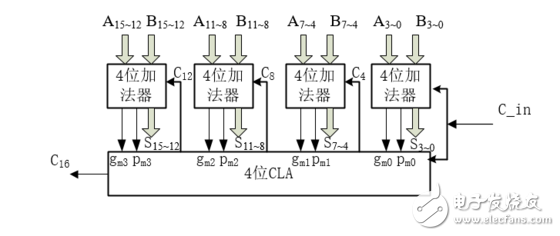
图5:16位超前进位加法器
至此,我们完成了16位超前进位加法器的设计。
要想设计32位超前进位加法器和设计16位超前进位加法器一样的方法,对16位超前进位加法器进行封装,引出16位加法器的进位产生信号Gx和进位传递信号Px即可。
第三步:设计32位超前进位加法器
因为我们已经有了16位超前进位加法器,并且已经引出了进位产生信号Gx和进位传递信号Px,那么我们只需要两个16位的超前进位加法器即可组成32位的加法器,但是超前部件CLA是4位的,意味着我们只需要用到CLA的低两位,所以整个32位的超前进位加法器模块图如下所示:
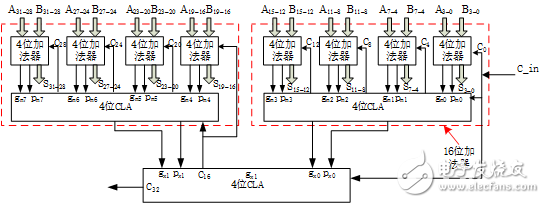
图6:32位超前进位加法器
至此,32位超前进位加法器完成。
回顾:此次32位超前进位加法器的设计以4位超前进位加法器和4位CLA部件为基础,采用组内和组间都是超前进位的方式,有效的减小了传统加法器串行进位导致的延迟问题,采用这种方法,只要设计合适位数的CLA部件,就可以设计任意位数的超前进位加法器,需要注意的地方就是进位产生信号和进位传递信号的理解,以及CLA部件的理解,下面附上此次设计的源码以及仿真波形图:
1位加法器:

4位CLA部件:

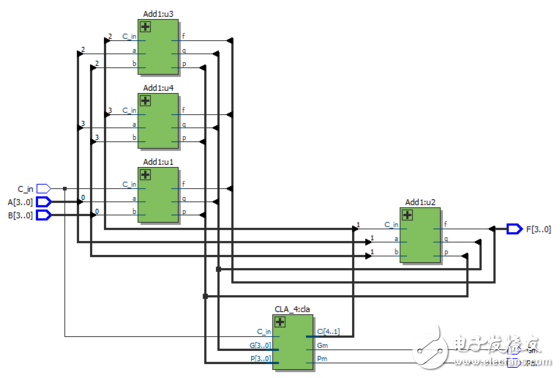
4位超前进位加法器:


4位超前进位加法器RTL视图:
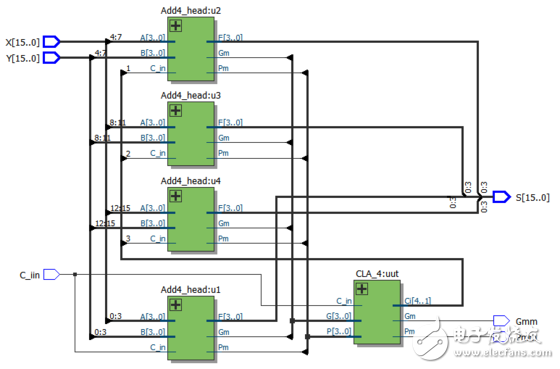
16位超前进位加法器:


16位超前进位加法器RTL视图:
32位超前进位加法器:

32位超前进位加法器RTL视图:
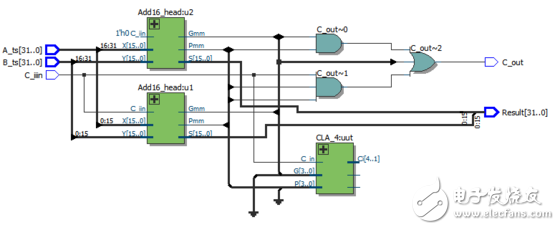
但是,我们发现如果在32位超前进位加法器中调用整个4位CLA,而我们仅仅只使用了两位,导致了资源的浪费,所以,我们修改代码如下:
*32位超前进位加法器:

*32位超前进位加法器RTL视图:
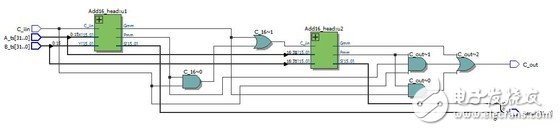
*32位超前进位加法器仿真激励:

*32位超前进位加法器仿真波形图:
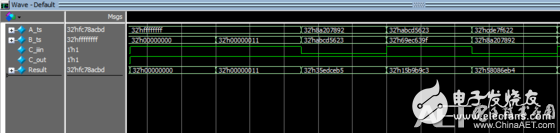
从波形图上可以看出,32位超前进位加法器功能正确,只要理解了设计的目的,以及设计的思想,实现这个加法器并不困难,所以理解很重要,希望能给正在学习计算机原理与组成的朋友帮上忙,谢谢!
如有不足的地方,还请指正!
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)