
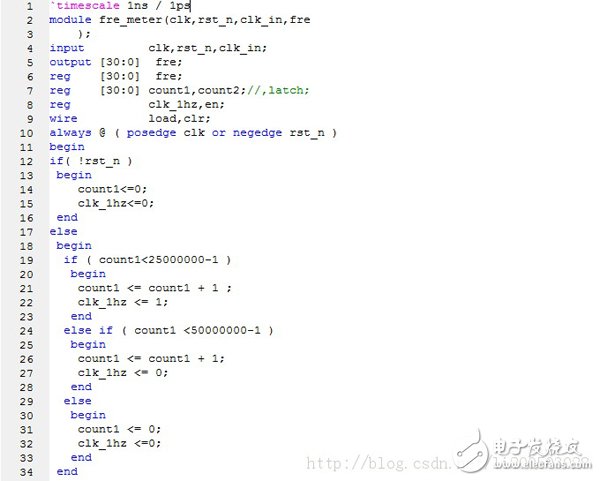
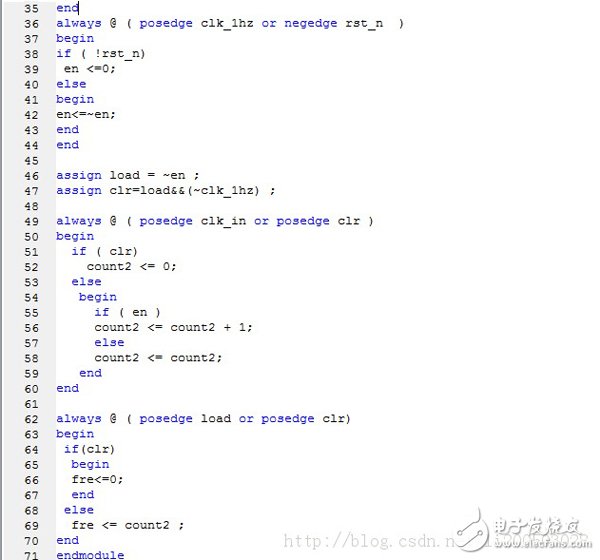
CORDIC是在没有专用乘法器(最小化门数量)情况下,一组完成特定功能的算法,包括平方、超越、Log、sin/cos/artan。原理为连续的旋转一个较小的角度,以一定精度逼近想要的角度。具体原理如下图所示:
2. Xilinx实现CORDIC IP核及性能测试 例1:无符号整数的平方 *** 作:
X_in[18:0],待平方的无符号整数,在nd(new data)为输入有效信号,输出x_out[9:0]及对应的使能信号rdy,其对应的波形图见下图。
(1)流水延迟
最下方为输入数据,最上方为输出求平方结果。从上图可以看到,从nd到rdy,间隔了5个时钟周期。
(2)时钟频率
在FX130-1芯片上综合时钟频率结果为2.8ns,。
例2:无符号整数的平方根 *** 作:在定制平方根IP核时,选取Unsigned FracTIon,将X_IN与X_OUT设置为相同bit位,19bit。以某项目为例,待平方数据需要19bit来表示。在项目中,因为待开放的数据表示图像坐标,因此为整数,数据格式为UFIX19_0,即用19bit表示数据,且小数位为零位。而CORDIX的输入要求为UFIX19_18,即19bit数据,其中18bit表示小数位,1bit整数。
在数据格式与CORDIC核的输入不一致情况下,需要对输出结果的bit位进行正确解释。
输入x_in=180: 000 0000 0000 1011 0100
输出x_dout=6869:000 0001 1010 1101 0101
解释:因为CORDIC期待的输入x_in为18bit小数,因此CORDIC的输出x_dout应为9bit小数,即13+0.25+0.125+0.03125+0.0078125+0.001953125 = 13.416。可以看出最小的精度可以保持到小数点第3位。在具体实现时,可以根据精度要求进行调整。
注:事实上,对于x_in代表的19个bit,18bit小数位,1bit小数位这样的数据格式下,x_dout不需要考虑移位便可得到正确解释;而其他格式下,则需要对x_dout进行相应的移位解释,比如上例,就是对x_dout进行了9bit的右移才得到了正确的估值。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)