基于FPGA的数控振荡器的设计

数控振荡器(NCO)因具有频率精度高、转换时间短、频谱纯度高以及频率相位易编程等特点，而被广泛应用于软件无线电数字上、下变频以及各种频率和相位数字调制解调系统中。
NCO是正交数字混频器的核心部分，它具有频率分辨率高、频率变化速度快、相位可连续线性变化和生成的正弦P余弦信号正交特性好等特点。而且NCO 的相位、幅度均已数字化，可以直接进行高精度的数字调制解调。随着数字通信的发展，传送的数据速率越来越高。如何得到一个可数控的高频载波信号是实现高速数字通信系统必须解决的问题。
NCO传统的实现方法主要有查表法、多项式展开法或近似法，但这些方法在速度、精度、资源方面难以兼顾。而采用CORDIC算法来实现超函数时，则无需使用乘法器，它只需要一个最小的查找表(LUT)，利用简单的移位和相加运算，即可产生高精度的正余弦波形，尤其适合于FPGA的实现。

数控振荡器原理

数控振荡器的作用是产生正交的正弦和余弦样本。 传统方法是采用查表法（LUT） , 即事先根据各个正余弦波相位计算好相位的正余弦值， 并按相位角度作为地址存储该相位的正余弦值， 构成一个幅度P相位转换电路（即波形存储器）在系统时钟的控制下， 由相位累加器对输入频率字不断累加， 得到以该频率字为步进的数字相位， 再通过相位相加模块进行初始相位偏移， 得到要输出的当前相位， 将该值作为取样地址值送入幅度P相位转换电路， 查表获得正余弦信号样本。NCO的目标是产生频率可变的正、余弦波样本，，(n=0，1，2...)。式中，fLO为本地振荡频率， fS为输入信号的采样频率。
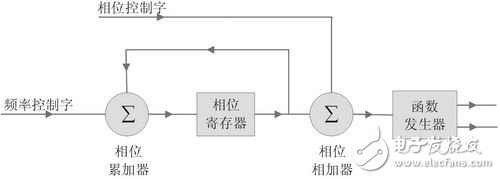
如图1 所示，NCO主要包括3个模块：
1. 相位累加器对输入频率控制字M不断累加， 得到以该频率字为步进的数字相位。
2. 相位相加器将相位寄存器中的数字相位与相位控制字相加， 得到偏移后的当前相位。　　
设系统的时钟频率为fc，频率控制字为M，相位寄存器位数为N，则数控振荡器输出信号频率为。根据Nyquist抽样定理，fs最大值为1/2fc，而在实际设计中，一般不应大于时钟频率的1/4。其频率分辨率为

根据此式，在系统时钟频率不变的情况下， 相位寄存器位数N越大， 产生信号的频率分辨率越高。

图1 数字控制振荡器结构图

3. 函数发生模块，对当前相位进行对应幅度转换后， 可以输出任意函数的波形。　　
对于一个相位位数为n，输出信号幅度位数为M 的数控振荡器，所需查找表大小为M ×2n。为了提高数控振荡器的频率分辨率，往往需要扩大波形存储器的容量，造成存储资源的大量消耗。而且当需要外挂RAM 来存储波形时，由于受到RAM读取速度的影响，数控振荡器的输出速率必然受到制约。因此，当需要设计高速、高精度的数控振荡器时，不宜采用查表法；而CORDIC算法的应用能够很好地解决这一问题。

CORDIC算法原理

CORDIC(坐标旋转数字计算机)算法是Jack Volder于1959年提出的，主要用于计算三角函数，双曲函数及其他的一些基本函数。J.Walther于1971年提出了统一的CORDIC形式。该算法的具体原理如下：如图2所示，初始向量a(x0，y0) (注意y0=0)经n次旋转后得到向量b(xN，yN)qi。设第i次旋转的角度为qi，根据J.Walther的推导得到迭代方程组：

通过选择tan(qi)=±2-i可以得到，x和y的方程现在可以利用一个简单的管状移位器和一个算术逻辑单元(ALU)来实现。此外，只需要使用一个相对简单的、事先计算好的反正切表，即可消除超函数的计算。

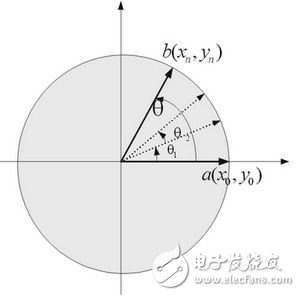
图2 CORDIC 算法原理示意图　　同时还要判断旋转的方向，以满足Z变量由初始值逐步趋于零，需要通过下式来引入和估计一个简单的符号变量：

经过上面2步，得到如下迭代方程：

则当N→ 时，迭代后结果为：(xi，yi)→(cos(q)，sin(q))。　　
综合以上推导可见，只要选取合适的N，计算出相应的初始值(x0，y0)，以及相对应的反正切值，就可以利用简单的移位加法 *** 作和流水线结构实现上述的迭代方程式，计算出已知角度Z的正、余弦值，且这样的电路结构非常易于FPGA实现。

应用MATLAB进行功能仿真和参数设计

FPGA设计流程中，应先利用MATLAB进行功能仿真，按照系统要求，以先验的方式确定系统参数，测试系统性能是非常必要的，可以有效提高FPGA硬件设计的效率和电路质量，避免不必要的重复劳动。　　
本系统采用40M的晶振，要求输出9.7M的正、余弦波，输出幅值为18位二进制数。在实际系统中，由于有限的相位字长和有限的量化电平，这些靠近期望分量的杂散信号会降低数字合成器的无杂散动态范围(SFDR)。本系统要求输出波形SFDR大于90dB。　　
通过将CORDIC迭代过程、相位计算，以及相位截断、量化字长等的误差等因素引入MATLAB仿真程序中，能够准确仿真出实际数字电路的输出波形。采用不同的参数，多次仿真后，确定选取迭代次数N=16，相位Z的范围为(-90，90)，是一个很好的平衡点。　　
仿真结果如图3所示，信号的频谱在9.7M达到峰值，说明生成的正弦波形其频率为9.7M，且最大信号幅度的有效值与最大杂散分量有效值分贝差接近100dB，即SFDR>90dB。可见，该结果完全符合NCO的系统设计要求，可以按照此设计参数进入到下一步FPGA数字电路实现。

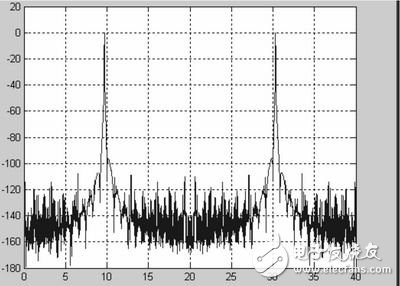
图3 基于CORDIC算法的NCO输出正旋信号频谱图

基于CORDIC的NCO的FPGA实现和验证

这一阶段的设计过程采用Verilog HDL编程，用Xilinx公司的FPGA设计工具实现。具体电路设计可分为两个部分。　　
第一部分为CORDIC迭代前模块，最终目的是输出当前相位，主要功能是进行相位累加、截断，以及按照上文的设计参数转换相位至(-90，90)之间，并给出相应的控制信号。图4中左边第一个模块anglepro即完成了上述功能。系统采用了32位的累加器，M值可由公式计算得到。下面只需进行相位的转换工作，对相位地址的高两位进行异或运算，当结果为0时，说明当前相位已经在设计区间(-90，90)之间;结果为1时则做简单的象限转换，将第二象限折入第一象限，第三象限折入第四象限，并输出控制信号t对最终输出的COS幅值取负。

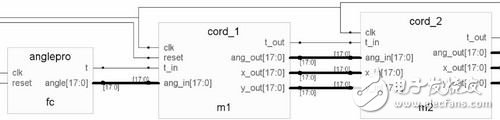
图4 Synplify Pro编译综合后RTL仿真图（局部）　　

第二部分为整个CORDIC算法的迭代过程，根据仿真结果，系统采取了16级迭代，X迭代初始值可由公式(5)算出K=0.6073，量化为18位二进制数后，得到幅值约为79600。在本次设计中，并没有将这些反正切角度量化值存入统一的LUT中，而是分别固化在每一级的迭代模块中，简化了数字电路结构。　　图4中cord_2是迭代过程中的一个典型迭代模块，其他15个迭代模块的核心结构与cord_2完全相同。如图5所示，流水线结构中，每一个模块(级)接受来自上一次迭代的Z角度值、X值、Y值，通过判断Z的符号对X、Y、Z做移位加减 *** 作，其迭代的核心部分只需要3个加减法器和2个移位器。

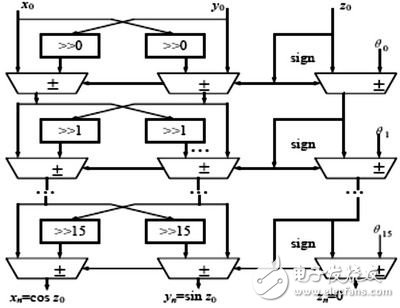
图5 CORDIC流水线结构图　　

采用这样的流水线结构，级级直接相连，每一级移位长度和反正切角度值的固化，也大大节省了FPGA实现时的寄存器数量。现实中只需要17个时钟周期的建立时间，就可输出第一个正、余弦值，然后连续输出波形的离散数值。　　
通过ModelSim仿真后，得到仿真波形如图6所示。　　

　　

图6 modelsim 仿真波形图　　

为了验证输出波形是否正确，本文采用了将量化后幅值还原与理想值比较的方法。如，第一个幅值对应的实际余弦值为131068/(2^17)≈0.99997。余弦值。取其中几组数据进行比较，如表1所示。　

　对比发现电路仿真后输出值与理想值很接近，得到了预期的正、余弦离散波形，验证了程序本身的正确性。结语采用CORDIC算法设计数控振荡器可以生成高精度数控振荡器而无需大容量的查找表，节省了大量的ROM资源，降低了功耗，仅采用移位寄存器和加法器结合流水线结构就可实现迭代过程。CORDIC算法所能达到的精度与所选取的迭代次数和 *** 作数位宽密切相关，利用三角函数的对称特性，配合少量LUT或逻辑电路，可以进一步设计出更高精度的数控振荡器。