
O 引言
在无线电接收机系统中,由于会受到发射机运动、接收机运动和标准频率随时间动态变化等因素的影响,其接收机接收信号往往会发生频率偏移,因而需要进行频偏校正。在扩频通信系统中,频偏校正电路能消除中频偏移对接收机扩频码的捕获以及数据解调性能的影响,从而提高接收机的性能。
频偏校正电路中通常需要根据给定相位产生余弦信号和正弦信号,其中最重要的实现技术是CORDIC (Coordinate RotaTIon Digital Computer,坐标旋转数字计算机)算法。本文将详细分析CORDIC算法的原理及其FPGA实现方法。
1 CORDIC算法的基本原理
在直角坐标系统中,假设有一向量(x,y),按逆时针方向旋转φ度得到向量(x1,y1),则两向量的代数关系为:
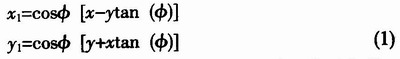
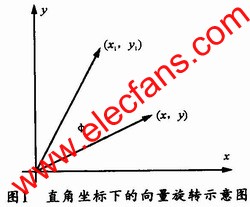
在式(1)中,如果让旋转的角度φ满足条件:tanφ=±2-i,则式(1)中的乘法 *** 作就可以转换为移位 *** 作,从而很容易在FPGA中实现。图l所示是直角坐标下的向量旋转示意图。若需要旋转的角度为θ,那么就可以通过n次旋转一系列预定角度αi来完成。
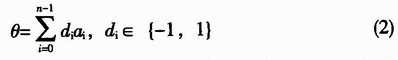
(2)式中,di表示每次旋转的方向为αi。由于每次旋转都为预定角度值,所以cosαi为常数,而n次旋转中每次迭代的处理可表示为:

一般情况下,当旋转的次数足够大时,Ki一般为常数。由于在实现时,可在最终的计算结果中再乘以这一常数,所以,可以去掉式(3)中的Ki,这样,迭代方程就仅含移位和加法运算,从而大大的简化了FPGA的实现复杂性。由于还需要一个方程决定di的符号,引入变量zi表示每次旋转预定角度的累加值:
这样,CORDIC算法的迭代方程可表示为:
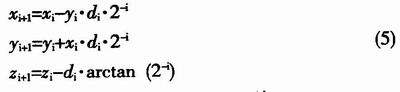
其最终结果为:

在频偏校正电路中,通常需要根据给定相位θ产生余弦信号cosθ和正弦信号sinθ。为了产生标准且无放大的正弦和余弦信号,可令输入向量的y分量(即yo)为0,x分量(即xo)为1/An,这样,式(6)就可简化为:

可见,经过上述处理就可将输入相位zo转换为标准的正弦和余弦信号。
2 CORDIC算法的FPGA实现
用FPGA实现CORDIC算法,最常用的方法有迭代算法和基于流水线的算法。CORDIC迭代算法只有一级迭代单元,在系统时钟的驱动下,可将迭代单元的输出作为本级的输入,并通过同一级迭代完成计算。迭代算法的硬件开销很小,但完成一次CORDIC运算需要多个时钟周期,其运算速度相对较慢。
在CORDIC流水线结构算法中,每一级CORDIC迭代运算都使用单独的运算单元,当流水线填满之后,每个时钟周期都马上会计算出一组结果,所以计算速度很快。
虽然流水线结构算法的计算速度很快,但其精度会受到流水线级数的限制。而要提高精度,就必须增加流水线级数,从而增大硬件开销,因此,流水线级数的选择要兼顾速度和精度的要求。
3 实现方案与仿真结果
3.1 实现方案
CORDIC算法的流水线流程图如图2所示,该方法采用7级流水线,故可大大提高计算速度。
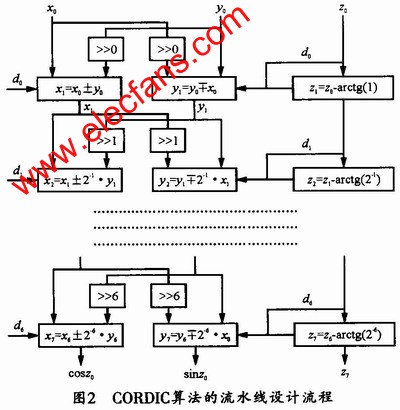
3.2 仿真结果
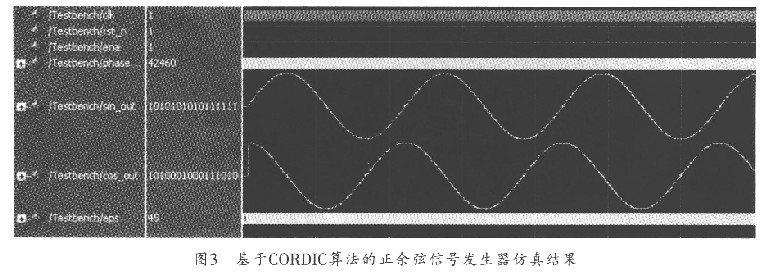
基于CORDIC算法的正余弦信号发生器的仿真结果如图3所示,由图3可见,该算法可以实现标准的正弦波和余弦波,并可直接作为频偏校正单元。
4 结束语
本文通过对CORDIC算法的工作原理进行分析,给出了基于CORDIC算法和FPGA实现数字频率校正的实现方案。仿真结果证明,该方法可以实现标准的正弦波和余弦波信号,可以直接作为频偏校正单元来对数字频率信号进行校正。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)