人工智能机器学习之受限玻尔兹曼机（RBM）算法

人工智能之机器学习主要有三大类：1）分类；2）回归；3）聚类。今天我们重点探讨一下受限玻尔兹曼机（RBM）算法。

受限玻尔兹曼机RBM在深度学习领域一直有重要应用，它是一种可用随机神经网络来解释的概率图模型，由Smolensky在1986年在玻尔兹曼机BM的基础上提出， 是玻尔兹曼机BM的一种特殊拓扑结构。

玻尔兹曼机BM原理起源于统计物理学，是一种基于能量函数的建模方法，能够描述变量之间的高阶相互作用，玻尔兹曼机BM的学习算法较复杂，但所建模型和学习算法有比较完备的物理解释和严格的数理统计理论作基础。

RBM概念：

以Hinton和Ackley两位学者为代表的研究人员从不同领域以不同动机同时提出BM学习机。BM是一种随机递归神经网络，可以看做是一种随机生成的Hopfield网络（请参见公众号之人工智能Hopfield网络）。BM是一种对称耦合的随机反馈型二值单元神经网络，由可见层和多个隐层组成，网络节点分为可见单元（visible unit）和隐单元（hidden unit），用可见单元和隐单元来表达随机网络与随机环境的学习模型，通过权值表达单元之间的相关性。

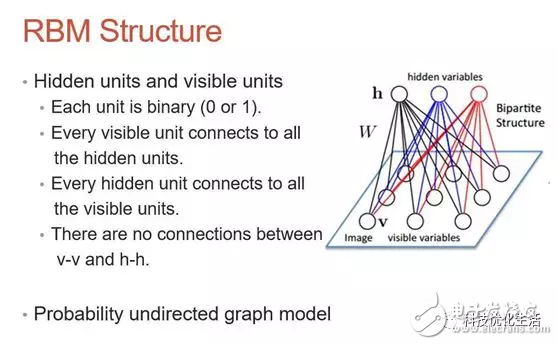
Smolensky提出的RBM由1个可见神经元层和1个隐神经元层组成，由于隐层神经元之间没有相互连接并且隐层神经元独立于给定的训练样本，这使直接计算依赖数据的期望值变得容易，可见层神经元之间也没有相互连接，通过从训练样本得到的隐层神经元状态上执行马尔可夫链抽样过程，来估计独立于数据的期望值，并行交替更新所有可见层神经元和隐层神经元的值。

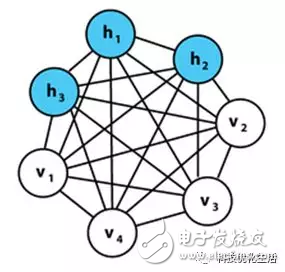
RBM引入：

受限玻尔兹曼机RBM是对玻尔兹曼机进行简化，使玻尔兹曼机BM更容易使用。玻尔兹曼机BM的隐元／显元和隐元／隐元之间都是全连接的，增加了计算量和计算难度，使用困难。而RBM则是对BM进行一些限制，使隐元之间没有连接，使得计算量大大减小，使用起来非常方便。

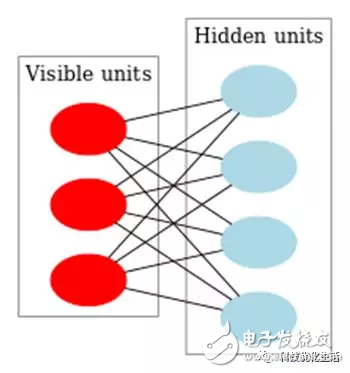
RBM原理：

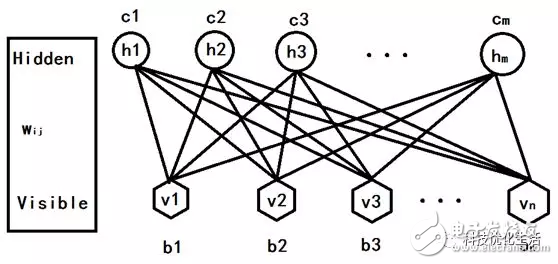
RBM参数如下：

1） 可视节点与隐藏节点直接的权重矩阵Wij；

2） 可视节点的偏移量b ＝ （b1，b2，．．．，bn）；

3） 隐藏节点的偏移量c ＝ （c1，c2，．．．，cm）；

这几个参数决定了RBM网络将1个n维的样本编码成1个m维的样本。假设RBM的隐元和显元的状态取1或0，则它的能量函数为：

根据吉布斯（Gibbs）分布：p（v，h）＝（1／Z）＊e［？E（v，h）］和上面的能量函数建立模型的联合概率分布。

可视节点状态只受m个隐藏节点影响，同理，每个隐藏节点也是只受n个可视节点影响。即：

其中，Z为归一化因子或配分函数，表示对可见层和隐藏层节点集合的所有可能状态的（能量指数）求和。Z计算复杂度非常高，无法直接计算，需要一些数学推导来简化计算量。

同理得到p（h）。

根据贝叶斯原理，知道联合概率和边缘概率，求得条件概率为：

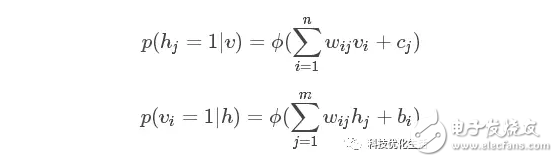
这里？是sigmoid函数。条件概率是根据隐元或显元的状态、权重W、偏差b或c来确定显元或隐元的状态。