
扩频通信是在民用和军用都有广泛应用的一种通信技术,自从其诞生就受到了广泛关注。 扩频通信中频谱的扩展是通过一个独立的伪随机序列来完成的。 其中 m 序列是最常用的一种伪随机码,本文在 matlab 平台上通过仿真,来研究如何用移位寄存器产生 m 序列,虽然 matlab 中有现成的 m 序列产生模块,但是它的相位是不可以调节的,而本文产生的 m 序列相位可以调节。 详细讲解了 m 序列的产生原理,和 matlab 仿真过程,最后给出了仿真结果,结果表明该方法是可行的。
扩频通信因其具有抗干扰、抗多径衰落、抗侦察等优点在通信领域中得到广扩频通信因其具有抗干扰、抗多径衰落、抗侦察等优点在通信领域中得到广泛应用。扩频序列的设计和选择是扩频通信的关键技术,扩频序列性能的优劣在很大程度上决定了通信系统的多址干扰和符号间干扰的大小,从而直接影响到系统的性能。因此,深入研究扩频序列的性质,构造设计具有良好相关性的扩频序列,来满足扩频系统的要求,是直接序列扩频系统的核心课题。白噪声是一种随机过程,它有极其优良的相关特性。但至今无法实现白噪声的放大、调制、检测、同步及控制等,而只能用类似于白噪声统计特性的伪随机序列来逼近它,并作为扩频系统的扩频码。
常见的伪随机序列有m 序列、GOLD 序列、M 序列、Walsh 序列等。m 序列是目前研究最为彻底的伪随机序列,m 序列容易产生, 有优良的自相关和互相关特性。序列是伪随机序列的一种情况。他可以在很多领域中都有重要应用。 由n级移位寄存器所能产生的周期最长的序列。这种序列必须由非线性移位寄存器产生,并且周期为2n(n为移位寄存器的级数)。
m 序列的产生原理产生 m 序列的线性反馈移位寄存器由寄存器加上反馈产生,n 阶线性移位寄存器的产生原理框图如图 1 所示。
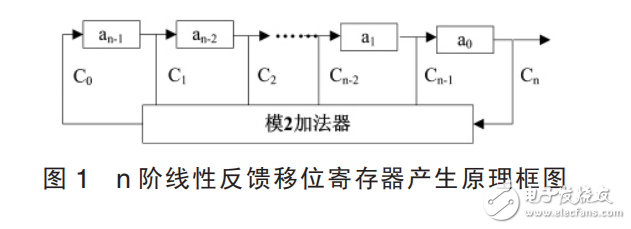
图 1 中 a0,a1, … ,an-1 为 n 个移位寄存器某时刻的状态,c0,c1,… ,cn 为移位寄存器的反馈系数,对应位置 ci 等于 1 表示有反馈,等于 0 表示无反馈,加法器采用模 2 相加。
反馈系数决定了反馈移位寄存器产生的 m 序列码型,对于图 1 中反馈移位寄存器,反馈逻辑为 c0,c1,…,cn,则
{an}=c1an-1+c2an-2+…+cna0
只要反馈逻辑 ci 确定,寄存器产生的序列就确定了。n 级移位寄存器产生的伪随机序列,其最长周期为 2n-1。
生成 m 序列的首要问题是要求得移位寄存器的特征多项式, 特征多项式必须为本原多项式, 本原多项式可以用matlab 软件编程求得,也可以直接查表获得,
m序列的性质扩展频谱通信要求扩频序列应具有较好的随机特性,而m序列既具有一定的随机特性,又具有一定的周期性,因而它是一种伪随机序列,m序列应具有移位相加特性、平衡特性和游程特性。
1.移位相加特性(线性叠加性)一个m序列{na}与其经任意次延迟移位后产生的另一个不同序列{kna}模2 相加,得到是仍是该m序列的延迟移位序列。例如1110100与向右移3 位后的序列1001110逐位模2相加后的序列为0111010 ,相当于原序列向右移1位后的序列,仍是m 序列。
2.平衡特性在m序列的每个21n周期中,“1”码元出现的数目为12n次,“0”码元出现的数目为121n次,即“0”的个数比“1”的个数少一个。
伪随机序列的平衡性是指序列中“1”的数目只比“0” 的数目多l。码的平衡性由码序列中的直流分量决定。平衡性好,则载波抑制度大,从而有利扩频通信的抗干扰能力以及保密和抗侦破能力。其物理意义是不平衡码会使扩频后的信号中出现一些稳定的信号,从而易于被检测而导致保密能力的降低。
3.游程特性游程是指在一个序列周期中连续排列的取值相同的码元的合称 ,所谓的游程长度就是一个游程中码元的个数。而m序列的分布特性为
1.m序列的一个周期(12nM)中,游程总数为12n;
2。当2n,且1 《游程长度k ≤n-2,长度为k的游程占游程总数的k21,其中0游程和1游程各占一半;
3。长度为1n的游程只有一个,是0游程; 4。长度为n的游程只有一个,是1有游程。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)