python – “round”ed编号乘以0.01会产生x.y00000000000001而不是x.y？

概述我问这个的原因是因为在 OpenERP中有一个验证它让我发疯： >>> round(1.2 / 0.01) * 0.011.2>>> round(12.2 / 0.01) * 0.0112.200000000000001>>> round(122.2 / 0.01) * 0.01122.2>>> round(1222.2 / 0.01) * 0.011222.2 如您所见,第二轮返回 我问这个的原因是因为在 OpenERP中有一个验证它让我发疯：

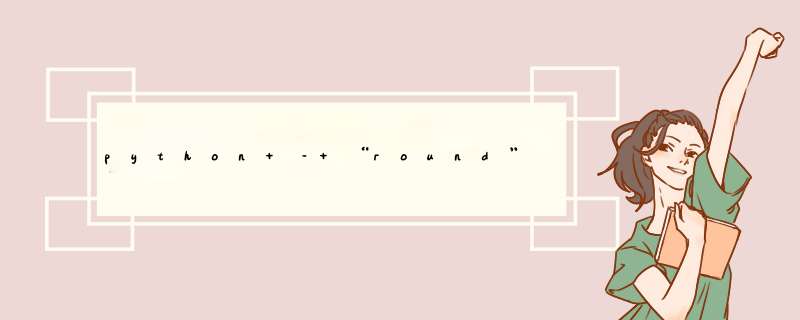
>>> round(1.2 / 0.01) * 0.011.2>>> round(12.2 / 0.01) * 0.0112.200000000000001>>> round(122.2 / 0.01) * 0.01122.2>>> round(1222.2 / 0.01) * 0.011222.2

如您所见,第二轮返回奇数值.

有人可以向我解释为什么会这样吗？

解决方法 事实上这与圆形无关,如果你只做1220 * 0.01,你可以看到完全相同的问题：

>>> 1220*0.0112.200000000000001

你在这里看到的是一个标准的浮点问题.

您可能想要阅读维基百科关于floating point accuracy problems的内容：

The fact that floating-point numbers cannot precisely represent all real numbers,and that floating-point operations cannot precisely represent true arithmetic operations,leads to many surprising situations. This is related to the finite precision with which computers generally represent numbers.

@H_301_36@

另见：

> Numerical analysis
> Numerical stability

浮点数值不稳定的一个简单例子：数字是有限的.假设我们在给定计算机或语言中的点之后保存4位数.0.0001乘以0.0001会导致低于0.0001,因此无法保存此结果！在这种情况下,如果你计算(0.0001 x 0.0001)/ 0.0001 = 0.0001,这个简单的计算机将无法准确,因为它试图先加倍而后才加倍除.在JavaScript中,除以分数会导致类似的不准确性.

总结

以上是内存溢出为你收集整理的python – “round”ed编号乘以0.01会产生x.y00000000000001而不是x.y？全部内容，希望文章能够帮你解决python – “round”ed编号乘以0.01会产生x.y00000000000001而不是x.y？所遇到的程序开发问题。

如果觉得内存溢出网站内容还不错，欢迎将内存溢出网站推荐给程序员好友。

欢迎分享，转载请注明来源：内存溢出

原文地址: http://outofmemory.cn/langs/1195203.html