10.对于MA(1)模型: Y, = e-0.5e,其一阶自相关系数是多少？

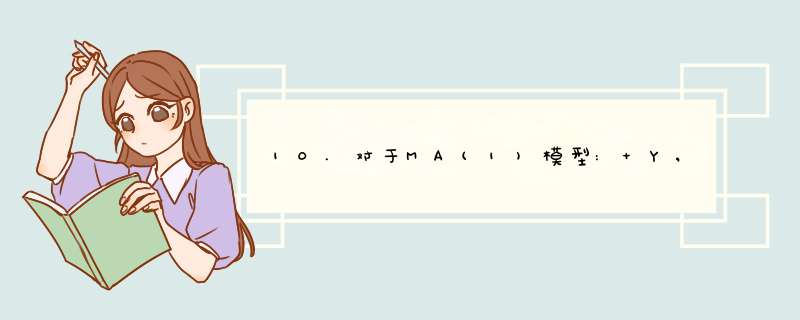
MA(1)模型是一种时间序列模型，它表示当前的观测值与前一个时间点的随机误差之间存在一种线性关系。具体而言，MA(1)模型可以表示为Yt = μ + et + θ1 et-1，其中μ是常数，et是白噪声误差项，而θ1则是MA(1)模型的参数，它表示前一个时间点的随机误差与当前观测值之间的影响程度。

要求MA(1)模型的一阶自相关系数，我们需考虑误差项et的相关性。因为MA(1)模型是一阶移动平均过程，所以它的自相关函数（ACF）为：

ACF(h) = 1 / (1 + θ12) if h = 1

ACF(h) = 0 if h > 1

其中，h表示滞后期，θ1表示MA(1)模型参数。

因此，MA(1)模型的一阶自相关系数可以简单地表示为：

ρ1 = ACF(1) = 1 / (1 + θ12)

例如，若 θ1 = -05，则：

ρ1 = 1 / (1 + (-05)2) = 067

因此，MA(1)模型的一阶自相关系数为067，这表示前一个时间点的随机误差与当前观测值之间存在较高的相关性。需要注意的是，MA(1)模型的自相关函数在滞后期大于1时为0，这表明模型的“记忆长度”很短，只有一个时间点。因此，MA(1)模型通常被用于描述具有短期相关性的时间序列数据。

F合=ma指的是牛顿第二定律，是求合力的。物体的加速度a跟物体所受的合外力F成正比，跟物体的质量m成反比，加速度的方向跟合外力的方向相同。F指给于物体加速度的力，M指加速物体的质量，A就是F力作用所产生的加速度。

牛顿第二定律适用范围

牛顿第二运动定律只适用于质点。对质点系，用牛顿第二运动定律时一般采用隔离法，或者采用质点系牛顿第二定律。

牛顿第二运动定律只适用于惯性参考系。惯性参考系是指牛顿运动定律成立的参考系，在非惯性参考系中牛顿第二运动定律不适用。但是，通过惯性力的引入。可以使牛顿第二运动定律的表示形式在非惯性系中使用。

牛顿第二运动定律只适用宏观问题。解决微观问题必须使用量子力学。当考察物体的运动线度可以和该物体的德布罗意波相比拟时，由于粒子运动不确定性关系式（即无法同时准确测定粒子运动的方向与速度），物体的动量和位置已经是不能同时准确获知的量了，因而牛顿动力学方程缺少准确的初始条件无法求解。

也就是说经典的描述方法由于粒子运动不确定性关系式已经失效或者需要修改。量子力学用希尔伯特空间中的态矢概念代替位置和动量（或速度）的概念（即波函数）来描述物体的状态，用薛定谔方程代替牛顿动力学方程（即含有力场具体形式的牛顿第二运动定律）。用态矢代替位置和动量的原因是由于测不准原理我们无法同时知道位置和动量的准确信息，但是我们可以知道位置和动量的概率分布，测不准原理对测量精度的限制就在于两者的概率分布上有一个确定的关系。

牛顿第二运动定律只适用低速问题。解决高速问题必须使用相对论。由于牛顿动力学方程不是洛伦兹协变的，因而不能和狭义相对论相容，因此当物体做高速移动时需要修改力、速度等力学变量的定义，使动力学方程能够满足洛伦兹协变的要求，在物理预言上也会随速度接近光速而与经典力学有不同。

1）用指针作为函数的参数，它的作用是将一个变量的地址传送到另一个函数中。

#include<stdioh>

void change(int a,int b) / 定义一个函数, 两个指针为函数的形参/

{

int temp;

temp=a; /函数的作用是 交换两个变量/

a=b;

b=temp

}

void main()

{

int c,d;

int e,f; /定义两个实参/

scanf("%d %d",&c,%d);

e=&c;

f=&d; /分别将c、d的地址赋给e、f/

if(c>d) change(e,f);

printf("%d %d\n",c,d);

}

2）指针也可以指向函数

格林函数是一种用来解有初始条件或边界条件的非齐次微分方程的函数。从物理上看，一个数学物理方程是表示一种特定的"场"和产生这种场的"源"之间的关系。例如，热传导方程表示温度场和热源之间的关系，泊松方程表示静电场和电荷分布的关系等等，格林函数对于解线性系统在实际光源激励下的响应问题具有很重要的意义。

MA模型具有可逆性，AR和MA之间可以互相转换，任何一个AR(p)模型都可以表示为MA(∞)，任何一个可逆的MA(q)模型也表示为一个AR(∞)模型。