Leetcode 剑指系列 Day 20 分治算法

Leetcode 剑指系列 Day 20 分治算法 1.剑指 Offer 07. 重建二叉树

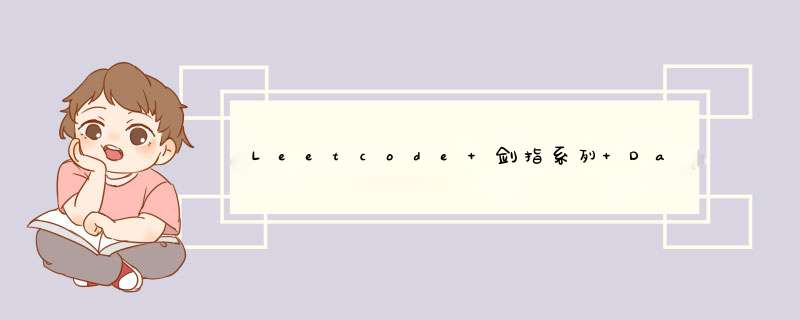
解题思路：

根据先序遍历和中序遍历的性质，每次遍历均可以确定一个中间节点和左右子树在数组中的位置，可以利用递归逐层建立树

算法过程：（prePosition为先序遍历的当前节点，inHead，inEnd为中序遍历下标范围）

class Solution {
public:
    TreeNode* rebuildTree(vector& preorder, vector& inorder, int prePosition, int inHead, int inEnd){
        //终止条件为inHead > inEnd
        if(inHead > inEnd) return NULL;
        TreeNode* ans = new TreeNode;
        ans->val = preorder[prePosition];
        int findMid;
        for(findMid = inHead; findMid <= inEnd; findMid++){
            if(inorder[findMid] == ans->val) break;
        }
        ans->left = rebuildTree(preorder, inorder, prePosition + 1, inHead, findMid - 1);
        ans->right = rebuildTree(preorder, inorder, prePosition + findMid - inHead + 1, findMid + 1, inEnd);
        return ans;
    }
    
    TreeNode* buildTree(vector& preorder, vector& inorder) {
        TreeNode* ans = rebuildTree(preorder, inorder, 0, 0, inorder.size() - 1);
        return ans;
    }
};

2.剑指 Offer 16. 数值的整数次方

解题思路（自下而上）：

根据题知得，要求x 的 n 次幂函数，可以把n看作二进制数，每次去掉n的最低位，若最低位为1则乘上x，否则不 *** 作，x翻倍，进入下一轮，直至n为0。

class Solution {
public:
    double myPow(double x, int n) {
        if(x == 0) return 0;
        long m = (long)n;
        if(n < 0){
            x = 1 / x;
            m *= -1;
        }
        double ans = 1.0;
        while(m > 0){
            if(m & 1) ans *= x;
            x *= x;
            m >>= 1;
        }
        return ans; 
    }
};

解题思路（自下而上）：

如代码所示

class Solution {
public:
    double myPow(double x, int n) {
        if(n == 0) return 1;
        if(n == 1) return x;
        if(n == -1) return 1 / x;
        double half = myPow(x, n / 2);
        double mod = myPow(x, n % 2);
        return half * half * mod;
    }
};

3.剑指 Offer 33. 二叉搜索树的后序遍历序列

解题思路：

根据最后一位的数值向前寻找分界点，传递的参数应当有下标范围，数组

以根节点为界，分别找到左右子树的范围与根节点数值进行比对

class Solution {
public:
    bool goVerify(vector& postorder, int left, int right){
        if(right <= left) return true;
        int board = right - 1;
        while(board >= 0 && postorder[board] > postorder[right]) board--;
        int fromBoard = board ;
        while(fromBoard >= left && postorder[fromBoard] < postorder[right]) fromBoard--;
        return (fromBoard == left - 1) && goVerify(postorder, left, board) && goVerify(postorder, board + 1, right - 1);
    }

    bool verifyPostorder(vector& postorder) {
        int num = postorder.size();
        return goVerify(postorder, 0, num - 1);
    }
};