经典字符dp

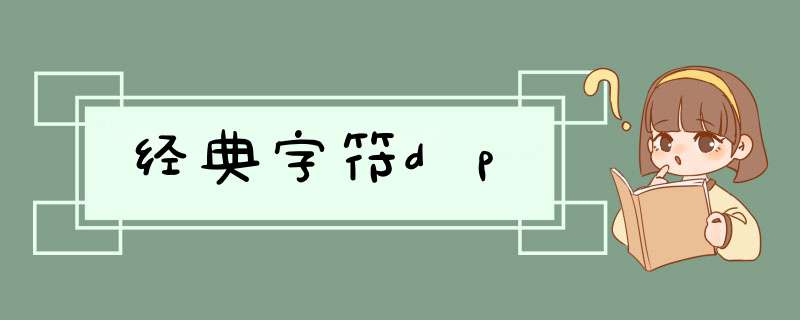
给三种 *** 作，删任意位置字符，添任意字符于任意位置，改任意字符为任意字符，求将串a变为串b的最小 *** 作数

dp四部曲：

1.定义子状态：进行多次 *** 作后将a变成b的所需 *** 作数

2.定义状态：dp[i][j]表示将串a的前i个字符转化为串b的前b个字符（提炼出的本质问题）

3.递推公式：对于前两个 *** 作即转化为dp[i-1][j]  dp[i][j-1]取较小的再加一分别表示删去最后a最后一个和添b最后一个的子问题，对于第三个 *** 作要讨论a[i-1]是否等于b[j-1]若等于再和dp[i-1][j-1]取min反之和其加一取min，这里将最优选择的策略转化为取最值。

4.去重：这里没有

5.注意初始化：如这里下标为0的位置要初始化

动态规划的核心就是找出一个无后部性的状态来递归或者说递推子状态处理。

昨天不影响未来，现在影响未来

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int inf=0x7f7f7f7f;
const int nn=1e5+50;
const double eps=1e-6;
inline int read() {
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
    while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
    return x*f;
}
inline void write(int  x) {
     if(x<0) putchar('-'),x=-x;
     if(x>9) write(x/10);
     putchar(x%10+'0');
}
int a[10005];
int dp[2005][2006];
int n,k;
int main ()
{
    string a,b;
    cin>>a>>b;
    int lena=a.length();
    int lenb=b.length();
    
    for(int i=1;i<=lena;++i)
        dp[i][0]=i;
    for(int j=1;j<=lenb;++j)
        dp[0][j]=j;
    for(int i=1;i<=lena;++i)
    {
        for(int j=1;j<=lenb;++j)
        {
            dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;
            if(a[i-1]==b[j-1])
                dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
        }
    }
    cout<