什么是Cayley图

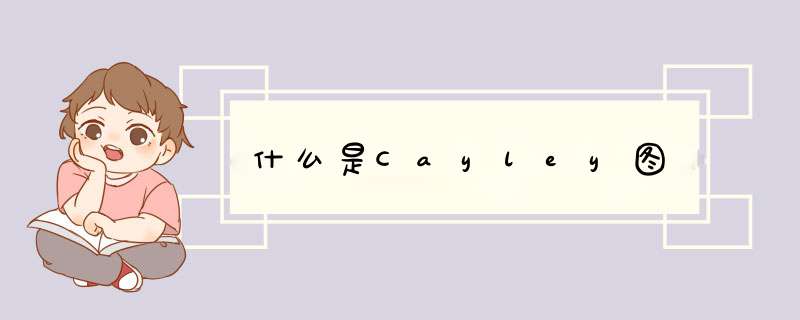
Cayley图，即凯莱图，以英国著名数学家阿瑟·凯莱命名。

通过把任何群(包括无限群比如 (R,+))都当作某个底层集合的置换群，把所有群都放在了同一个根基上。因此，对置换群成立的定理对于一般群也成立。

Cayley图通过把任何群(包括无限群比如 (R,+))都当作某个底层集合的置换群，把所有群都放在了同一个根基上。因此，对置换群成立的定理对于一般群也成立。

Cayley图说明用n-1条边将n个一致的顶点连接起来的连通图的个数为n^(n-2)，也可以这样理解，将n个城市连接起来的树状公路网络有n^(n-2)种方案。所谓树状，指的是用n-1条边将n个顶点构成一个连通图。当然，建造一个树状的公路网络将n个城市连接起来，应求其中长度最短、造价最省的一种，或效益最大的一种。Cayley定理只是说明可能方案的数目。

《离散数学》补充练习题（20110530）

1、将下列命题符号化

（1）小李边读书边听音乐

（2）现在没下雨,可也没出太阳,是阴天

2、证明等价关系：

3、概述求解主合取范式的主要方法和步骤,并求公式 的主合取范式

4、将下列论证用命题符号表示,然后求证逻辑推论是否成立

如果天热则蝉鸣叫,如果蝉鸣叫则小王不睡觉,小王游泳或睡觉,所以如果天热则小王游泳

5、将下列语句用谓词公式表示

（1）不劳动者不得食

（2）每个人的祖父都是他父亲的父亲

6、给定集合 , 均是 上的二元关系, ,

（1）画出 的关系图；

（2）写出 的关系矩阵；

（3）写出 所具有的性质；

（4）求

7、设 是集合 上的二元关系证明

8、简述传递闭包的定义,并求 上关系 的传递闭包

9、列出色数 为的三个图：

10、 阶完全图的色数为：

11、 阶树的色多项式为：

12、 阶完全图的色接多项式为：

13、如下图所示的图的邻接矩阵为,关联矩阵为

14、设 阶图的各顶点的度分别为 ,则称 为该图的度序列度序列为 的简单图是

15、是否存在度序列为 , 的简单图若存在,给出一个图；若不存在,请说明理由

16、画出如下图的所有生成子图

17、设图 如下图所示,求该图的生成树个数

18、已知图G（V、E）,画出G－V5,G－v3v4,G[{v2,v3,v5}],G[{v3v4,v4,v6,v7v8}]

G：

19、已知图G的邻接矩阵 ,画出G,并求出度序列

20、证明：偶图G的任意子图H仍为偶图

21、证明：设图G（V、E）的度序列为（ ）,边数为q,则

22、证明：整数序列（6,6,5,4,3,3,1）不可能为一个简单图的图序列

23、证明顶点度数均为 的简单连通图是圈

23、若图G是 不连通的,则其补图GC是连通的

24、证明：设 是由 和 两个连通分支组成的图,则其色多项式

25、证明：设 是由 和 两个连通分支组成的图,则其色数

26、设图G（V、E）且|V|＝p,|E|＝q,则G为树当且仅当G为连通的且p＝q＋1

27、证明：图G为树当且仅当G的任意两个不同顶点之间存在唯一的一条路

28、画出全部非同构的6阶树

29、利用Cayley公式计算图G的生成树数目（写出演算过程）

G：

30、下列图是否为Enler图

G1： G2：

31、证明：设 为 条边的 阶连通简单图且 ,则 包含圈

32、证明：非平凡树的最长路的起点和终点均为悬挂点

33、证明：恰好有两个悬挂点的树是一条路

34、证明：图G为非平面图

G：

35、给出下图G的一个最大匹配（最大对集）

G：

36、设图G有完美匹配,则G为偶数阶图

37、证明：路至多有一个完美匹配

38、写出p（≥1）阶树T的色多项式,并确定T的色数

39、写出5个阶轮图W5的色多项式,并求χ（w5）

W5：

40、设G为任一偶图,则χ（G）≤2

41、证明：非平凡连通偶图 的色数为

42、证明圈 的色数为 或

43、证明：设 为具有 条边的 阶极大平面图,则

44证明：在空间中,不可能有这样的多面体存在,它们有奇数个面,而它们的每个面又都有奇数条边

证明：假设存在这样的多面体,将这多面体的面用顶点表示,当且仅当两个面有公共棱时,在相应的顶点间连一边,得图G按题意,G有奇数个奇顶点显然,这样的图不存在,故这样的多面体是不存在的

45 A wolf, a goat and a cabbage are on one bank of a river A ferryman wants to take them across, but since his boat is small, he can take only one of them at a time For obvious reasons, neither the wolf and the goat nor the goat and the cabbage can be left unguarded How is the ferryman going to get them across the river

在一河岸有狼、羊和卷心菜,农夫要将它们渡过河去,但由于他的船太小,每次只能载一样葡萄东西,并且,狼和羊,羊和卷心菜都不能在无人照看的情况下留在一起问农夫有无办法将它们渡过河去若有,给出其实施办法

人、狼、羊、菜四种东西的任意组合,共有24=16种情况,其中狼羊菜、羊菜、狼羊三种情况不允许,因而这三种情况的余：人、人狼、人菜三种情况也不会出现这样,岸上只能有如下10种情况：

人狼羊菜、 人狼羊、 人狼菜、 人羊菜、 人羊、

空、 菜、 羊、 狼、 狼菜

将这10种状态各用一个点表示,且两种状态的两个点有边相连当且仅当该两种状态可用载人（或加一物）的渡船互相转换于是可得下图：

我们的问题就转化为求一条从“人狼羊菜”到“空”的路从而可求得渡河办法

数学的一个分支学科（主要学科）。它是以微积分方法为基本工具，以函式（映射、关系等更丰富的内涵）为主要研究对象，以极限为基本思想的众多数学经典分支及其现代拓展的统称。简称分析。

基本介绍 中文名 ：分析学 外文名 ： ysis 含义 ：分析学和函式论等 基本内容 ：古典分析、现代分析等 狭义广义,历史发展,分支,学科联系, 狭义广义 狭义的分析学（ ysis），指数学分析。以微分学、积分学、级数论、实数理论为其基本内容。 广义的分析学（ ysis）。极限的概念不仅是微积分的核心，也是许多其他学科的重要思想。微积分是近代数学的基础，从它已产生许多新的数学分支，如微分方程、函式论、变分法、泛函分析等，统称为广义的分析学。 历史发展 20世纪初年以前，一般将全部数学分为三大基本分支：分析学、代数学和几何学。当然，对于现代数学，已难于做如此的概括。像微分方程和机率论等学科，它们的创立都与分析密切相关，但由于它们各有独特的研究对象，从而发展了各自的庞大系统，不能继续将它们归属于分析学。一般而论，现代分析可分为实分析、复分析和包括泛函分析在内的抽象分析三大部分，它的研究对象已不限于函式，研究方法也日益综合。 分析这个学科名称，大约是由牛顿（Newton）最早引入数学的，因当时微积分被看做代数的扩张，“无穷”的代数，而“分析”与“代数”同义。今天它所指虽然更广，但仍然只是对所含学科方法上共同特点的概括，而且愈来愈不容易与代数、几何的方法完全分清了。 分析学中最古老和最基本的部分是数学分析。它是在17世纪为了解决当时生产和科学提出的问题，经过许多数学家的努力，最终由牛顿和莱布尼茨（Leibniz）创立的。但是为分析建立严格逻辑基础的工作却迟至19世纪方才完成。此后，数学分析才成为一个完整的数学学科。数学分析是最早系统研究函式的学科，它所研究的虽说基本上只是一类性质相当好的函式——区间上的连续函式，但无论在理论上或套用方面至今都有重要意义。在理论方面，数学分析是分析学科的共同基础，也是它们的发源地。现代分析的诸多分支中，有一些在其发展初期曾经是数学分析的一部分（例如变分法、傅立叶分析以至复变函数论等），而另一些则是在数学分析的完整体系建立以后，由于各种需要，在对数学分析中的某些问题的深入研究和拓广之中发展起来的，像实变函式论、泛函分析和流形上的分析就属于这种情况。 19世纪末到20世纪初，由于某些数学分支（例如傅立叶分析）和物理等学科发展的需要，不但促使数学分析中函式可积的概念逐步明确，还进一步要求将积分推广到更广的函式类上去，希望积分运算更加灵活方便。同时，在对数学分析中各个基本概念之间的关系的继续探讨中（例如，微分和积分互为逆运算在一般意义上是否成立），人们也感到必须突破数学分析的限制。 勒贝格 在这方面，20世纪初，由勒贝格（Lebesgue）提出的积分理论有重大意义，而实变函式论的中心内容就是勒贝格积分的理论。作为黎曼积分的推广，勒贝格积分不仅可积函式类广，还具有可数可加性等良好性质，积分号下求极限的条件也较宽松，它的理论已经发展得充分完备，因而更适合数学各分支及物理的需要。由于勒贝格可积函式的空间（函式类）的完备性，使它在数学理论上占据黎曼积分所不可能有的重要地位。实变函式论同数学分析一样，也研究函式的连续性、可微性、可积性这些基本性态，但由于套用了集合论的方法，使它有可能研究一般点集上的函式，从而研究的结果比数学分析更广、更完善。因此，实变函式论也成为分析学各分支（特别是泛函分析等近代分支）的共同基础之一。在关于微分和积分是否互为逆运算的问题上，勒贝格积分的结果就比黎曼积分情形进了一步。但是，为了彻底解决这个问题，后来又有人提出过多种更广的积分理论，例如，当儒瓦积分和佩龙积分，最后由广义当儒瓦积分（1916年）对前述问题作了肯定的回答。然而，这些积分除了在特定的理论问题上有重要意义外，远不如勒贝格积分普遍适用。勒贝格积分是建立在勒贝格测度的基础之上的，后者向抽象方面进一步发展，又促使对于测度的系统研究形成独立的学科，这就是测度论。测度是面积、体积概念的推广，它和积分概念始终紧密相联，测度论的思想和理论在现代分析中是十分重要和很有用的。 分支 分析学的诸多经典分支，或分析学各学科的经典部分中，数学分析、单复变函数论和实变函式论具有基础性质，它们全面研究所论函式的基本性态。除此以外，它的大多数分支主要从某个侧面去研究函式。例如，调和分析主要研究函式用傅立叶级数（或傅立叶变换）表示的问题，并利用这种表示去研究函式的性态。事实证明，这是研究函式重要而有效的途径，它的思想和方法在许多数学分支中用到。函式逼近论研究用某些性质良好的函式逼近一般函式的可能性及误差（逼近阶）等性质，以及反过来用这些性质去刻画函式。凸分析主要研究一类重要的非线性函式——凸函式。经典的变分法研究泛函的极值问题，这里的泛函一般限于含有变元函式的积分，因此也可以说它还是研究函式的。在今天，这些以函式为主要对象的经典学科，仍然是分析学的重要组成部分。 写满公式的纸 交错群A_5的一个Cayley图（一种群的图示） 分析学的各经典学科多形成于17至19世纪之间，但除去数学分析、单复变函数论和实变函式论的基础内容已基本定型之外，其他的都在不断拓展它们的研究领域。象调和分析是从一元函式的傅立叶级数理论发展起来的，原来也称为傅立叶分析，但现今它的主要内容却是多元（函式的）调和分析和群上的调和分析（抽象调和分析），从研究的问题到方法上都有很大变化。在一些问题中，傅立叶变换逐渐被别的由它演变来的更有力的工具替代，因而很难继续用后一名称来概括它的全部内容。函式逼近论在初期主要讨论用代数的或三角的多项式逼近连续函式的有关问题，而现今所考虑的作为逼近工具的特殊函式和被逼近函式的类型都丰富多了。从这些学科的发展中可以看到，它们的研究对象正随之发生变化。与其说它们研究的仍然是函式，不如说主要是某些函式空间（函式类）和运算元（变换）更为恰当，有关研究已推广到了群、流形或其他抽象的基域上。位势论的发展有类似的情况。经典的位势论研究牛顿位势（一类偏微分方程边值问题的积分形式的解），而现代位势论中所讨论的一般位势，实质上与牛顿位势相似，无非是关于某种测度对适当的核的特殊积分运算元。群上的位势论也正在发展。对诸如此类的空间及运算元抽象、系统的研究属于泛函分析。它是20世纪初发展起来的学科，是经典分析在近代的拓展。 另一个新的分析学科是流形上的分析，一般认为它在20世纪中期才形成独立分支。它研究定义在流形上的函式，而流形上一般没有统一坐标，只在每点存在与欧氏空间中的开集同胚的邻域，因此，流形上的局部分析与经典的欧氏空间的分析相仿，整体分析则复杂得多，流形上的分析指的就是后者（或称大范围分析）。它可以在流形这个全新背景之下，研究与各个经典分析学科相应的问题，是经典分析的现代拓展。例如，大范围变分法充实了大范围分析的内容，它既是变分法的现代发展，又可以看做流形上的分析的一部分。由于流形上的函式的性态与流形本身的几何、拓扑性质密切相关，从而可以认为，流形上的分析是分析学与几何、拓扑、代数互相综合的产物。这也反映了现代数学发展的特点。 学科联系 各学科密切联系、相互渗透与综合是现代数学发展的重要特点。现代分析学的发展，除了依靠本身的基础之外，特别吸收和利用了集合论、代数以及拓扑的思想和方法。已经提到的泛函分析和流形上的分析的形成和发展就是如此。再如，抽象调和分析和大范围变分法等，它们的基本问题还属于经典分析的推广，可是方法上完全离不开代数和拓扑，并都已形成独立的分支。离散化的方法在分析中用得越来越多，一些抽象代数的概念和理论被用到过去与它无缘的分析问题中。至于分析学内部各学科的结合就更多了，特别是泛函分析与其他经典学科的结合，现时已很平常。广义函式论已普遍成为许多经典分析领域的研究工具。前面提到过调和分析等学科对某些函式空间及运算元的研究，这方面问题的提法和研究方法都有很多借鉴于泛函分析，并依赖于运算元论的成果，又有各自的特点，代表了各自的发展方向，从而对泛函分析也是补充和发展。 戈弗雷·哈罗德·哈代 其次，实分析与复分析的结合，也很引人注目。哈代空间理论的发展，可以作为这方面的典型例子。在20世纪初，它完全是复变函数论的一部分，20世纪60年代以后，在此基础上发展了多元哈代空间的实变理论，这又促进了多复变函数论在这方面的研究。分析学还与其他许多数学学科在内容上有复杂的交叉，思想和方法上联系密切。其中一些是长期存在而又有所发展的，如调和分析、变分法、位势论与微分方程的关系，而新近的则如调和分析、位势论与机率论的联系都是很突出的例子，这对双方学科的发展都很有影响。这类相互间的联系、渗透和综合已经十分普遍和深入，这就使得分析学的研究者，或者只想学习和了解现代分析的人，都应有多方面的数学知识基础。 分析学属基础数学范畴。作为纯粹数学学科，分析学的发展虽不以在科学技术中的套用为直接目的，然而随着时代的发展，很多抽象的数学概念和理论都在物理以及现代科技中找到实际背景或套用。微积分的创立，本来就有物理方面的源泉，所以分析学与物理的紧密联系从牛顿时代就开始了。以后在不同时代建立的一些分析学科（如变分法、位势论等）发展了这种关系。现代分析中对于某些运算元的研究以及流形上的分析理论等在物理中的套用就更深入了。同时，电子计算机的发展不仅扩大了数学的套用范围，另一方面，而且也为数学理论研究提供了有力工具。在分析学方面，函式逼近论的某些方向（如样条函式逼近等）曾显得十分活跃，就因为它在与计算机相联系的计算数学中有广泛的套用。又由于计算机使许多最最佳化问题有可能实际求解，进而推动了变分法和凸分析的某些方向的发展。傅立叶分析在图象和信号处理的套用中，一直是重要的工具，现时发展起来的小波分析借助于计算机，在许多科学分支（如天体物理和地球物理等）中得到更广泛的套用。其实，计算机对数学的影响，决不限于某些套用及与它直接相关的理论方面。计算机的发展已直接影响到数学教学，并将进一步影响到整个数学的发展。现时由于机器证明有新的突破，人们日益注目于数学推理的构造性以及数学的机械化，这对于分析学这样的纯粹数学学科，无例外地将有越来越大的影响。 冯·诺依曼 总之，分析学自微积分创立以来，历经三百余年的发展，至今形成一个庞大的分支体系。它影响和改变了整个数学的面貌。在现代科学技术的推动下，分析学仍在蓬勃地向前发展。

物联网时代，大量的数据从不同的设备传感器产生，单机数据库系统肯定无法存储这么大量的数据，在选择数据库方面，肯定要选择具有分布式能力存储的数据库。

在物联网时代，数据之间还有一个非常重要的特性，那就是数据之间的关联性。不同的数据从相互连接的互联网设备传感器中产生，由于不同的传感器相互连接，协同工作和采集数据，如何将大量具有相互关联的数据保存在数据库，这里我推荐使用图数据库来进行存储。

图数据库相对于其他数据库来说，最大的优势就是查询数据之间的关联性会更加快速，消耗的时间会更短。打个比方，在社交网络中，我们想要查询在用户A的粉丝中，粉丝关注了B的用户。如果使用传统关系型数据库来存储用户的关注关系，在上面的数据统计中，要使用两层Join才能算出结果，而关系型数据库Join *** 作会很慢。使用图型数据库存储数据的话，图中的点为用户，边为用户的关注关系，在查询A的粉丝，同时粉丝也关注B的用户，只需要遍历两层关注关系就能很快查询到结果。

图数据库也属于NoSql数据库的一种，常用的图形数据库有，JanusGraph、Neo4j、Cayley、dgraph。不同的图数据库，底层实现也不尽相同。

JanusGraph是一种分布式图数据库，由Java语言开发，可以使用Hadoop生态存储系统作为数据源，构建出数据大图。是TiTan图数据库的开源版本，支持事务的ACID。

Neo4j是一种单机的图数据库，其优势就是能够快速安装并且使用，便于新同学上手。你的数据量一般不大的话，我推荐使用Neo4j，直接使用Neo4j相关的API就可以将数据模型图构建而出，然后使用Neo4jCypher查询语言，就可以分析数据，Cypher是一种类SQL的语言。

Cayley和Dgraph都是使用Go语言实现的图数据库，Go语言的最大特性就是其编译速度和开发便捷性，Cayley和Dgraph都支持分布式存储，不过都不支持SQL语言查询数据，Dgraph不支持事务，而Cayley支持事务，不过在开源社区，Dgraph比Cayley更加活跃，这里优先建议使用Dgraph作为物联网的存储数据库。

总体来说，在物联网时代，一定要学会使用图数据库，在分析大量数据之间的关联性时，图数据库就能够派上用场，图数据库最大的优势就是分析不同数据之间的关联性。

以上就是关于什么是Cayley图全部的内容，包括:什么是Cayley图、求图论例题 最小生成树,拓扑,最短路等等的例题,其他图论题也行,联赛提高组就行了.、分析学详细资料大全等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！