MATLAB的拟合函数polyfit 的程序代码是什么啊

polyfit.m 在MATLAB安装目录下 \toolbox\matlab\polyfun

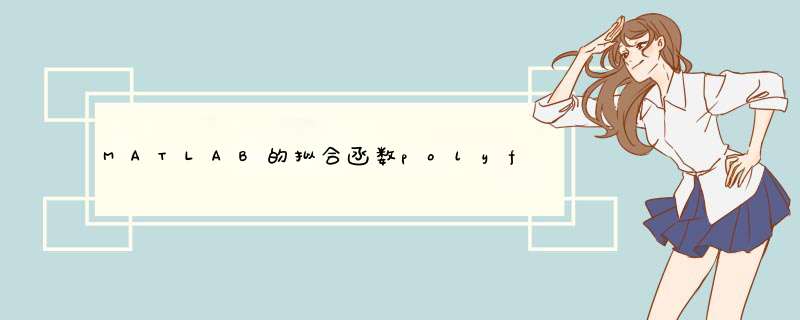
function [p,S,mu] = polyfit(x,y,n)

%POLYFIT Fit polynomial to data.

% P = POLYFIT(X,Y,N) finds the coefficients of a polynomial P(X) of

% degree N that fits the data Y best in a least-squares sense. P is a

% row vector of length N+1 containing the polynomial coefficients in

% descending powers, P(1)*X^N + P(2)*X^(N-1) +...+ P(N)*X + P(N+1).

%

% [P,S] = POLYFIT(X,Y,N) returns the polynomial coefficients P and a

% structure S for use with POLYVAL to obtain error estimates for

% predictions. S contains fields for the triangular factor (R) from a QR

% decomposition of the Vandermonde matrix of X, the degrees of freedom

% (df), and the norm of the residuals (normr). If the data Y are random,

% an estimate of the covariance matrix of P is (Rinv*Rinv')*normr^2/df,

% where Rinv is the inverse of R.

%

% [P,S,MU] = POLYFIT(X,Y,N) finds the coefficients of a polynomial in

% XHAT = (X-MU(1))/MU(2) where MU(1) = MEAN(X) and MU(2) = STD(X). This

% centering and scaling transformation improves the numerical properties

% of both the polynomial and the fitting algorithm.

%

% Warning messages result if N is >= length(X), if X has repeated, or

% nearly repeated, points, or if X might need centering and scaling.

%

% Class support for inputs X,Y:

% float: double, single

%

% See also POLY, POLYVAL, ROOTS.

% Copyright 1984-2004 The MathWorks, Inc.

% $Revision: 5.17.4.5 $ $Date: 2004/07/05 17:01:37 $

% The regression problem is formulated in matrix format as:

%

%y = V*por

%

% 3 2

%y = [x x x 1] [p3

% p2

% p1

% p0]

%

% where the vector p contains the coefficients to be found. For a

% 7th order polynomial, matrix V would be:

%

% V = [x.^7 x.^6 x.^5 x.^4 x.^3 x.^2 x ones(size(x))]

if ~isequal(size(x),size(y))

error('MATLAB:polyfit:XYSizeMismatch',...

'X and Y vectors must be the same size.')

end

x = x(:)

y = y(:)

if nargout >2

mu = [mean(x)std(x)]

x = (x - mu(1))/mu(2)

end

% Construct Vandermonde matrix.

V(:,n+1) = ones(length(x),1,class(x))

for j = n:-1:1

V(:,j) = x.*V(:,j+1)

end

% Solve least squares problem.

[Q,R] = qr(V,0)

ws = warning('off','all')

p = R\(Q'*y) % Same as p = V\y

warning(ws)

if size(R,2) >size(R,1)

warning('MATLAB:polyfit:PolyNotUnique', ...

'Polynomial is not uniquedegree >= number of data points.')

elseif condest(R) >1.0e10

if nargout >2

warning('MATLAB:polyfit:RepeatedPoints', ...

'Polynomial is badly conditioned. Remove repeated data points.')

else

warning('MATLAB:polyfit:RepeatedPointsOrRescale', ...

['Polynomial is badly conditioned. Remove repeated data points\n' ...

' or try centering and scaling as described in HELP POLYFIT.'])

end

end

r = y - V*p

p = p.' % Polynomial coefficients are row vectors by convention.

% S is a structure containing three elements: the triangular factor from a

% QR decomposition of the Vandermonde matrix, the degrees of freedom and

% the norm of the residuals.

S.R = R

S.df = length(y) - (n+1)

S.normr = norm(r)

/**********************************************

*Author :wacs5

*DATE :20090408(YYYMMDD)

*Functtion :多项式拟合polyfit

**********************************************/

#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

#include <math.h>

main()

{

int i,j,m,n=7,poly_n=2

double x[7]={1,2,3,4,6,7,8},y[7]={2,3,6,7,5,3,2}

double a[3]

void polyfit(int n,double *x,double *y,int poly_n,double a[])

system("cls")

polyfit(n,x,y,poly_n,a)

for (i=0i<poly_n+1i++)/*这里是升序排列，Matlab是降序排列*/

printf("a[%d]=%g\n",i,a[i])

getch()

}

/*==================polyfit(n,x,y,poly_n,a)===================*/

/*=======拟合y=a0+a1*x+a2*x^2+……+apoly_n*x^poly_n========*/

/*=====n是数据个数 xy是数据值 poly_n是多项式的项数======*/

/*===返回a0,a1,a2,……a[poly_n]，系数比项数多一（常数项）=====*/

void polyfit(int n,double x[],double y[],int poly_n,double a[])

{

int i,j

double *tempx,*tempy,*sumxx,*sumxy,*ata

void gauss_solve(int n,double A[],double x[],double b[])

tempx=calloc(n,sizeof(double))

sumxx=calloc(poly_n*2+1,sizeof(double))

tempy=calloc(n,sizeof(double))

sumxy=calloc(poly_n+1,sizeof(double))

ata=calloc((poly_n+1)*(poly_n+1),sizeof(double))

for (i=0i<ni++)

{

tempx[i]=1

tempy[i]=y[i]

}

for (i=0i<2*poly_n+1i++)

for (sumxx[i]=0,j=0j<nj++)

{

sumxx[i]+=tempx[j]

tempx[j]*=x[j]

}

for (i=0i<poly_n+1i++)

for (sumxy[i]=0,j=0j<nj++)

{

sumxy[i]+=tempy[j]

tempy[j]*=x[j]

}

for (i=0i<poly_n+1i++)

for (j=0j<poly_n+1j++)

ata[i*(poly_n+1)+j]=sumxx[i+j]

gauss_solve(poly_n+1,ata,a,sumxy)

free(tempx)

free(sumxx)

free(tempy)

free(sumxy)

free(ata)

}

void gauss_solve(int n,double A[],double x[],double b[])

{

int i,j,k,r

double max

for (k=0k<n-1k++)

{

max=fabs(A[k*n+k])/*find maxmum*/

r=k

for (i=k+1i<n-1i++)

if (max<fabs(A[i*n+i]))

{

max=fabs(A[i*n+i])

r=i

}

if (r!=k)

for (i=0i<ni++) /*change array:A[k]&A[r] */

{

max=A[k*n+i]

A[k*n+i]=A[r*n+i]

A[r*n+i]=max

}

max=b[k] /*change array:b[k]&b[r] */

b[k]=b[r]

b[r]=max

for (i=k+1i<ni++)

{

for (j=k+1j<nj++)

A[i*n+j]-=A[i*n+k]*A[k*n+j]/A[k*n+k]

b[i]-=A[i*n+k]*b[k]/A[k*n+k]

}

}

for (i=n-1i>=0x[i]/=A[i*n+i],i--)

for (j=i+1,x[i]=b[i]j<nj++)

x[i]-=A[i*n+j]*x[j]

}

有两种方法可以画平滑曲线，第一种是拟合的方法，第二种是用spcrv。

其实原理应该都一样就是插值。下面是源程序，大家可以根据需要自行选择，更改拟合的参数。

clc,clear

a = 1:1:6  %横坐标

b = [8.0 9.0 10.0 15.0 35.0 40.0]%纵坐标

plot(a, b, 'b')   %自然状态的画图效果

hold on

%第一种，画平滑曲线的方法

c = polyfit(a, b, 2)  %进行拟合，c为2次拟合后的系数

d = polyval(c, a, 1)  %拟合后，每一个横坐标对应的值即为d

plot(a, d, 'r')       %拟合后的曲线

plot(a, b, '*')       %将每个点 用*画出来

hold on

%第二种，画平滑曲线的方法

values = spcrv([[a(1) a a(end)][b(1) b b(end)]],3)

plot(values(1,:),values(2,:), 'g')

---