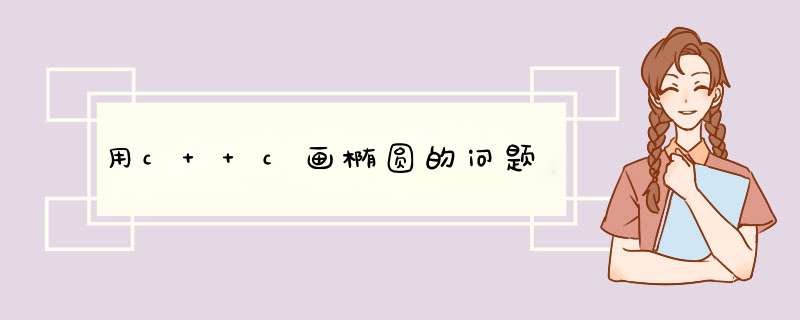
BOOL Ellipse(
HDC hdc,// handle to DC
int nLeftRect, // x-coord of upper-left corner of rectangle
int nTopRect, // y-coord of upper-left corner of rectangle
int nRightRect, // x-coord of lower-right corner of rectangle
int nBottomRect // y-coord of lower-right corner of rectangle
)
详细说明参看MSDN或百度一下
以下为matlab采用最小二乘法的椭圆拟合程序:function a = fitellipse(X,Y)
% FITELLIPSE Least-squares fit of ellipse to 2D points.
%A = FITELLIPSE(X,Y) returns the parameters of the best-fit
%ellipse to 2D points (X,Y).
%The returned vector A contains the center, radii, and orientation
%of the ellipse, stored as (Cx, Cy, Rx, Ry, theta_radians)
%
% Example: Run fitellipse without any arguments to get a demo
if nargin == 0
% Create an ellipse
t = linspace(0,2)
Rx = 300
Ry = 200
Cx = 250
Cy = 150
Rotation = .4 % Radians
x = Rx * cos(t)
y = Ry * sin(t)
nx = x*cos(Rotation)-y*sin(Rotation) + Cx
ny = x*sin(Rotation)+y*cos(Rotation) + Cy
% Draw it
plot(nx,ny,'o')
% Fit it
fitellipse(nx,ny)
% Note it returns (Rotation - pi/2) and swapped radii, this is fine.
return
end
% normalize data
mx = mean(X)
my = mean(Y)
sx = (max(X)-min(X))/2
sy = (max(Y)-min(Y))/2
x = (X-mx)/sx
y = (Y-my)/sy
% Force to column vectors
x = x(:)
y = y(:)
% Build design matrix
D = [ x.*x x.*y y.*y x y ones(size(x)) ]
% Build scatter matrix
S = D'*D
% Build 6x6 constraint matrix
C(6,6) = 0C(1,3) = -2C(2,2) = 1C(3,1) = -2
% Solve eigensystem
[gevec, geval] = eig(S,C)
% Find the negative eigenvalue
I = find(real(diag(geval)) <1e-8 &~isinf(diag(geval)))
% Extract eigenvector corresponding to negative eigenvalue
A = real(gevec(:,I))
% unnormalize
par = [
A(1)*sy*sy, ...
A(2)*sx*sy, ...
A(3)*sx*sx, ...
-2*A(1)*sy*sy*mx - A(2)*sx*sy*my + A(4)*sx*sy*sy, ...
-A(2)*sx*sy*mx - 2*A(3)*sx*sx*my + A(5)*sx*sx*sy, ...
A(1)*sy*sy*mx*mx + A(2)*sx*sy*mx*my + A(3)*sx*sx*my*my ...
- A(4)*sx*sy*sy*mx - A(5)*sx*sx*sy*my ...
+ A(6)*sx*sx*sy*sy ...
]'
% Convert to geometric radii, and centers
thetarad = 0.5*atan2(par(2),par(1) - par(3))
cost = cos(thetarad)
sint = sin(thetarad)
sin_squared = sint.*sint
cos_squared = cost.*cost
cos_sin = sint .* cost
Ao = par(6)
Au = par(4) .* cost + par(5) .* sint
Av = - par(4) .* sint + par(5) .* cost
Auu = par(1) .* cos_squared + par(3) .* sin_squared + par(2) .* cos_sin
Avv = par(1) .* sin_squared + par(3) .* cos_squared - par(2) .* cos_sin
% ROTATED = [Ao Au Av Auu Avv]
tuCentre = - Au./(2.*Auu)
tvCentre = - Av./(2.*Avv)
wCentre = Ao - Auu.*tuCentre.*tuCentre - Avv.*tvCentre.*tvCentre
uCentre = tuCentre .* cost - tvCentre .* sint
vCentre = tuCentre .* sint + tvCentre .* cost
Ru = -wCentre./Auu
Rv = -wCentre./Avv
Ru = sqrt(abs(Ru)).*sign(Ru)
Rv = sqrt(abs(Rv)).*sign(Rv)
a = [uCentre, vCentre, Ru, Rv, thetarad]
Elliptic-curve cryptography ( ECC ) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields . ECC requires smaller keys compared to non-ECC cryptography (based on plain Galois fields ) to provide equivalent security
参考文章
[TOC]
数学上,椭圆曲线为一代数曲线,形如
$$y^2 = x^3 + ax + b$$
并且该曲线无奇点(尖点或自相交),判别式$\Delta = -16(4a 3+27b 2)$不为0.
在椭圆曲线中添加无穷远点 O ,由于曲线关于y轴对称,假设P为曲线上一点,则P关于y轴的对称点定义为-P。无穷远点的对称点为其自身,因此 O = -O
定义 + 运算,假设P,Q,-R在曲线上,则 P + Q = -R ->P + Q + R = O 其中-R与P,Q共线。
定义数乘 *
$$
nP = \underbrace{P + P + \cdots + P}_{n\ \text{times}}
$$
$$y^2 = x^3 + ax+ b \bmod{p}$$
下图是曲线$y^2 = x^3 -7x+10\bmod{p}$,其中p为19,97,127,487时的点集。可看到点集关于y = p/2对称。
定义直线$ax+bx+c \equiv 0 \bmod{p}$,既等间距的直线族。
若点集中P,Q,-R三点在同一直线上,则 P+Q+R = O
$(9 9^{-1})\ mod\ 23 = 1 = (9 18)mod\ 23$
$P = (x_p,y_p)$
$Q = (x_q,y_q)$
$R = (x_r,y_r)$
$$P+Q = -R$$
公式
$$
x_r = (m^2-x_p-x_q) \bmod{p}
$$
$$
y_r = [y_p+m(x_r-x_p)]\bmod{p}
$$
若$P \neq Q $则$m = (y_p - y_q)(x_p-x_q)^{-1}\bmod{p}$
若$P = Q$则$m = (3x_p 2+a)(2y_p) {-1}\bmod{p}$
点集中点的数量称为椭圆曲线的阶数,有快速算法 Schoof's algorithm
$$nP = \underbrace{P + P + \cdots + P}_{n\ \text{times}}$$
例如曲线$y^2 \equiv x^3 + 2x + 3 \bmod{97}$的点$P = (3,6)$
通过上边例子可以看出P与数乘,最终只有有限的循环出现的几个结果$kP = (k\bmod{5})P$,这五点在加法运算下封闭。这五点构成了 循环子群 ,其中P称为 generator or base point of the cyclic subgroup
Cyclic subgroups are the foundations of ECC and other cryptosystems.
the order of is the smallest positive integer $n$ such that $nP = 0$ . In fact, if you look at the previous example, our subgroup contained five points, and we had $5P = 0$.
The order of $P$ is linked to the order of the elliptic curve by Lagrange's theorem , which states that the order of a subgroup is a divisor of the order of the parent group .
In other words, if an elliptic curve contains $N$ points and one of its subgroups contains $n$ points, then $n$ is a divisor of $N$, so $N\ mod\ n \equiv 0$
For example, the curve $y^2 = x^3-x+3$ over the field $F_{37}$ has order $N = 42$ . Its subgroups may have order 1,2,3,6,7,14,21 and 42 . If we try $P = (2,3)$ can see that $1P\neq0,2P\neq0,3P\neq0,6P\neq0,7P=0,$ so the order of is 7.
对于ECC算法,我们希望子群阶数足够高。所以通常我们选择一条椭圆曲线,计算其阶数,并选择一个较大的因子作为子群的阶数,最终找到一个基点。
在Lagrange's theorem中令$h =N/n$,称$h$为 cofactor of the subgroup 余因子
由于$nP = 0$所以$h(nP) = 0 = n(hP)$
现在考虑$n$是素数,令$G =hP$,则生成一个以$G$为基点的n阶子群
现已知点PQ在椭圆曲线上,如何确定整数$k$使得$Q =kP$ ?这个问题被称为椭圆曲线的离散对数问题,这个问题被认为是一个困难的问题,目前还没有多项式时间解决方法。
在密码学中Digital Signature Algorithm (DSA), the Diffie-Hellman key exchange (D-H) and the ElGamal algorithm都与该问题有关。
ECC问题相比其它几个问题更难以解决。
Our elliptic curve algorithms will work in a cyclic subgroup of an elliptic curve over a finite field.
得到算法六元组$(p,a,b,G,n,h)$
在前面提到离散对数问题非常困难,但也不是所有的都困难,有些类型的椭圆曲线就非常脆弱,有非常快速的方法解决,例如$p = hn$时就有多项式时间解决的方法。
怎样保证曲线是安全的呢?
为了解决这个问题,我们需要再附加一个参数 seed $S$,这是一个随机数涌来生成参数a和b,或者基点G再或者所有的参数。这些参数通过hash函数生成,hash容易计算但是难以逆推。
椭圆曲线的生成通过随机数生成,这使得曲线足够的随机。
如果我们知道$d$和$G$,计算$H$非常容易。但是如果我们仅知道$H$和$G$,计算$d$将非常困难,因为这是离散对数问题。
ECDH是 Diffie-Hellman algorithm 的一种变体,更像密钥交换协商而不是加密。应用场景:双方需要安全的交换信息,即使第三方拦截到也无法破译。这是TSL背后的一个原则。
$$S=d_AH_B=d_A(d_BG)=d_B(d_AG)=d_BH_A$$
Alice使用私钥$d_A$签名文件,Bob使用Alice的共钥$H_A$来确认。
ECDSA作用在消息的hash上,而不是直接作用在消息上。Hash函数可以选择密码学安全的。hash需要被截断为和子群阶数$n$所占bit一样的长度,例如前边n是256bit,那么hash也需要是256bit,截断后的hash定义为整数$z$
$(r,s)$ 就是签名。
Alice对hash $z$ 使用私钥 $d_A$ 和随机数 $j$签名。Bob使用Alice的共钥 $H_A$验证。
验证签名,验证签名需要Alice的共钥 $H_A$ 截断的hash $z$,以及签名 $(r,s)$.
如果 $r=x_P\bmod{n}$则是合法的
$$
\begin{array}{rl}
P &= u_1 G + u_2 H_A \
&= u_1 G + u_2 d_A G \
&= (u_1 + u_2 d_A) G
\end{array}
$$
再带入 $u_1,u_2$的定义
$$
\begin{array}{rl}
P &= (u_1 + u_2 d_A) G \
&= (s^{-1} z + s^{-1} r d_A) G \
&= s^{-1} (z + r d_A) G
\end{array}
$$
这里省略了$mod\ n$,因为在子群阶数为$n$,所以相当于自动对n取模。由$s = k^{-1} (z + rd_A) \bmod{n}$推出$k = s^{-1} (z + rd_A)\bmod{n}$.
$$
\begin{array}{rl}
P &= s^{-1} (z + r d_A) G \
&= k G
\end{array}
$$
这与签名算法第二步生成的是同一个点P,接下来验证是否满足生成算法第三步即可验证签名。
当使用ECDSA进行数字签名时,k要相当饱满。如果每次签名都使用相同的k,或者k是可预测的,那么就被找出私钥。 This is the kind of mistake made by Sony a few years ago. ,PS3只能运行Sony使用ECDSA签名过的程序,但问题是Sony使用了固定的k
这样可以轻松的找出Sony的私钥$d_S$,只要买两份签名的游戏,取出他们的hash ($z_1 z_2$),和两份签名$(r_1,s_1),(r_2,s_2)$,以及椭圆参数。
$$
s = k^{-1}(z+rd_S)\bmod{n}\Rightarrow d_S = r^{-1}(sk-z)\bmod{n}
$$
我们认为离散对数问题是非常困难的,但是并没有数学上的证明。目前解决离散对数问题由三种方法,假设$Q=xP$,求x
随意假定$x=am+b$
$$
\begin{array}{rl}
Q &= xP \
Q &= (am + b) P \
Q &= am P + b P \
Q - am P &= b P
\end{array}
$$
选择一条标准曲线 prime192v1 ,$n$=0xffffffff ffffffff ffffffff 99def836 146bc9b1 b4d22831,$\sqrt{n} \approx 7.9\cdot10 {28}$,每个点需要32Byte存储,大概总共需要$2.5\cdot10 {30}$byte,这比全世界存储还多。而且 prime192v1 还是一个低阶曲线。
使用量子算法可让复杂度降低$O((\log{n})^3)$
$y 2+xy=x 3+ax^2+1$ a为0或1,拥有$2^m$点,其中m为素数
$x 2+xy=x 3+x^2+b$ b是随机生成的整数
这两条曲线计算较快。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)