伯努利概型的Cnk怎么求。？例如 C上4下5怎么求…？

5！/(5-4)!=5432=120
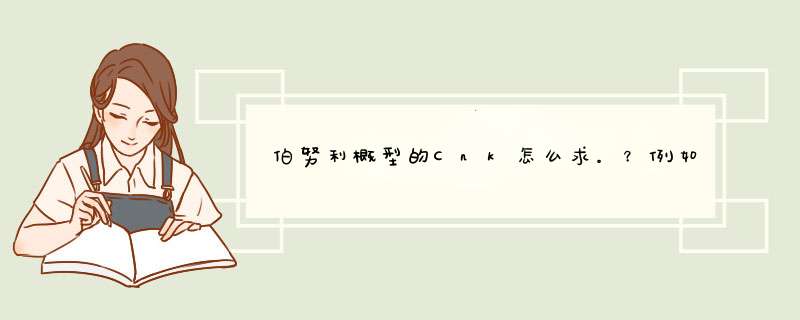
n在下，k在上
Cnk可看为在n个空格中任意选k个空格，如C5,4是在5个中选4个，那么第一个有5种可能，第二个有4种可能···第四个有2种可能，所以C5,4=5432=120；
Cnk=n!/(n-k)!=n（n-1)···（n-k+1）

p+ρgh+(1/2)ρv^2=c　式中p、ρ、v分别为流体的 压强、 密度和 速度；h为铅垂高度；g为 重力加速度；c为 常量。
伯努利原理往往被表述为p+1/2ρv2+ρgh=C，这个式子被称为伯努利方程。式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，C是一个常量。它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。 需要注意的是，由于伯努利方程是由机械能守恒推导出的，所以它仅适用于粘度可以忽略、不可被压缩的理想流体
我只能找到这些，我也不懂

将三个不同的球随机地放入四个不同的杯子中去，有4^3=64法，

其中杯子中球的最大个数为1的有A(4,3)=24法，

杯子中球的最大个数分别为2的：从4个杯子中取2个杯子有C(4,2)法，把3个球中的2个球、1个球放入这两个杯子有A(3,2)法,共C(4,2)A(3,2)=36法，

杯子中球的最大个数分别为3的有4法，

所求概率依次为3/8,9/16,1/16

概率是度量偶然事件发生可能性的数值。假如经过多次重复试验(用X代表)，偶然事件(用A代表)出现了若干次(用Y代表)。以X作分母，Y作分子，形成了数值(用P代表)。在多次试验中，P相对稳定在某一数值上，P就称为A出现的概率。如偶然事件的概率是通过长期观察或大量重复试验来确定，则这种概率为统计概率或经验概率。

扩展资料

在一定条件下，重复做n次试验，nA为n次试验中事件A发生的次数，如果随着n逐渐增大，频率nA/n逐渐稳定在某一数值p附近，则数值p称为事件A在该条件下发生的概率，记做P(A)=p。这个定义称为概率的统计定义。

在历史上，第一个对“当试验次数n逐渐增大，频率nA稳定在其概率p上”这一论断给以严格的意义和数学证明的是雅各布·伯努利。

从概率的统计定义可以看到，数值p就是在该条件下刻画事件A发生可能性大小的一个数量指标。

解答：
设10台机床中实际开动的机床数为随机变量x，
每台机床开动的概率是P=15/60=1/4
∴ x～B（10，1/4）．
∴ P(x=k)=C(10,k)(1/4)^k(3/4)^(10-k)
50kW电力可以同时供给5台机床开动，
∴10台机床同时开动的台数不超过5台时都可以正常工作．
∴所求概率是P(x≤5)
∴ 所求概率
P=C(10,0)(3/4)^10+C(10,1)(1/4)(3/4)^9+C(10,2)(1/4)^2(3/4)^8+C(10,3)(1/4)^3(3/4)^9
+C(10,4)(1/4)^4(3/4)^6+C(10,5)(1/4)^5(3/4)^5
(以下是按计算器的工作了。)

---