高中数学均匀分组问题

解：1先从6本中取2本给甲，再从4本中取2本给乙，剩余2本给丙，共
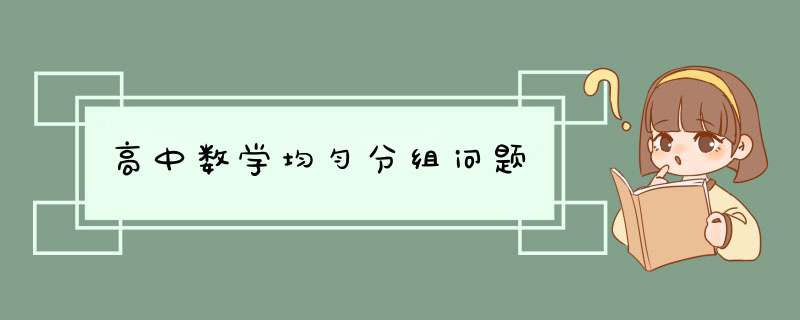
C2,6C2,4C2,2=90种
2平均分堆问题，先从6本中取2本做一堆，再从4本中取2本做一堆，剩余2本一堆，但需注意平均分堆时要除以堆数的全排列数，不平均分堆则不用除，共
C2,6C2,4C2,2/A3,3=15种
3不区分人，即可看做是平均分为3份，等同于问题2，也为15种。
希望能够理解。

一、知识点介绍

平均分组，就是将不同的元素平均分成几组，问有多少种不同的方法数。

如：将ABCD四人平均分成两组，有几种分法

我们可以尝试枚举：

第一种：ABCD

第二种：ACBD

第三种：ADBC

第四种：CDAB

第五种：BDAC

第六种:BCAD

通过枚举，我们可以发现第一种和第四种其实是一种分法，第二种和第五种是一种分法，第三种和第六种是一种分法。因此，四人平均分成两组共有三种分法。

平均分成的组，不管他们的顺序如何，都是一种情况，因此我们可以得出一个结论：有n个不同的元素，平均分成m个组，每个组都有k(k=)个元素，则有种不同的方法数。

二、例题讲解

例1将10名运动员平均分成两组进行对抗赛，问有多少种不同的分法

A120

B126

C240

D252

答案B

解析第一步，本题考查排列组合问题，属于基础排列组合。

第二步，由平均分成两组可知，此题属于平均分组问题，将10人平均分成两组，每组5人，直接套用平均分组公式可得

因此，选择B选项。

例2某单位工会组织桥牌比赛，共有8人报名，随机组成4队，每队2人。那么小王和小李恰好被分在同一队的概率是:

A1/7

B1/14

C1/21

D1/28

答案A

解析第一步，本题考查概率问题，属于其他概率问题。

第二步，根据平均分组公式，8人平均分成4组，每组两人，有种方法;

小王和小李被分在同一组，则剩下的6人平均分成3组，每组两人，有种方法。

第三步，小王和小李被分在同一组的概率为÷=。

因此，选择A选项。

例3某市举办足球邀请赛，共有9个球队报名参加，其中包含上届比赛的前3名球队。现将这9个球队通过抽签的方式平均分成3组进行单循环比赛，则上届比赛的前3名球队被分在同一组的概率是：

A1/21

B1/28

C1/63

D1/84

答案B

解析第一步，本题考查概率问题，属于其他概率问题。

第二步，根据平均分组公式，9人平均分成3组，每组三人，有种方法;

上届比赛的前3名球队被分在同一组，则剩下的6人平均分成2组，每组三人，有种方法。

第三步，上届比赛的前3名球队被分在同一组的概率为÷=。

因此，选择B选项。

这里举一个简单的例子说明一下
甲乙丙丁4个人平均分成2组
那么有（4C2）（2C2）/（2A2）=3种情况，很明显甲乙，甲丙，甲丁（两组中一组的情况）三种情况，因为选好1组以后，剩下一组就不用分了，自动分成了一组
而如果不除以分组的阶乘，那么就会有重复出现，4C22C2中，有甲乙，甲丙，甲丁，乙丙，乙丁，丙丁（两组中一组的情况），这时候甲乙和丙丁一组会与丙丁和甲乙一组重复，所以要排除重复的情况：2组的全排列2A2
同理，6个人abcdef均分为3组
任选一组ab，ce，df，按6C24C22C2的算法，会有3A3种情况重复，即ab，ce，df三组的全排列
所以6人分3组答案为6C24C22C2/3A3

由题设，放球可分为两个步骤：（一）先从4个盒子里取出2个盒子放球，取法有C(4,2)=6种。（二）把4个球分为两份，即(1,3)和(2,2)(①)当分法为(1,3)时，只要从4个球里拿出1个球，即可分为两份，这样分没有重复，分法为C(4,1)=4种。（②）当4个球均分为两份时，分法为C(4,2)/A(2,2)=3种。此处为何要除以A(2,2)呢？这是因为有重复，如a,b,c,d4个元素均分为两份，(ab,cd,),(ac,bd),(ad,bc),仅有3种分法，若按C(4,2)计算就有6种分法。重复了，故除以2。∴把4个球分为两份，分法有C(4,1)+C(4,2)/A(2,2)=4+3=7种。拿出两个盒子，每种分球法又有两种放法，∴总的分法有C(4,2)×{2[C(4,1)+C(4,2)/A(2,2)]}=6×[2(4+3)]=6×14=84种。

1除数是一位数的整数除法
整数除法高位起,除数一位看一位;
一位不够看两位,三个步骤试着除;
除到哪位商那位;不够商一0占位。
余数要比除数小,然后再除下一位。
2除数是两位数的整数除法
整数除法高位起,除数两位看两位;
两位不够看三位,三个步骤试着除;
除到哪位商那位;不够商一0占位。
余数要比除数小,然后再除下一位。
3多位数的整数除法
整数除法高位起,除数几位看几位;
几位不够加一位,三个步骤试着除;
除到哪位商那位;不够商一0占位。
余数要比除数小,然后再除下一位
试商与调商:
1试商技巧:表内乘法口诀、口算能力、估算能力是提高试商准确性的关键。
2调商:每一次试商过程中,①当被除数不够除时(不够减),说明商大了,商就要调小;
②当除得的余数大于除数时,说明商小了,商就要调大。

同样是4个，从abcd中，挑出ab剩下cd是一种情况，挑出cd剩下ab是另一种情况，所以不用除以二。
而分组的时候，抽出ab从而分成ab、cd两组是一种情况，抽出cd从而分成cd、ab两组是与上一种情况一样的情况，所以要除以二。

---