LeetCode每日一题之托普利茨矩阵

LeetCode每日一题之托普利茨矩阵 LeetCode每日一题之托普利茨矩阵

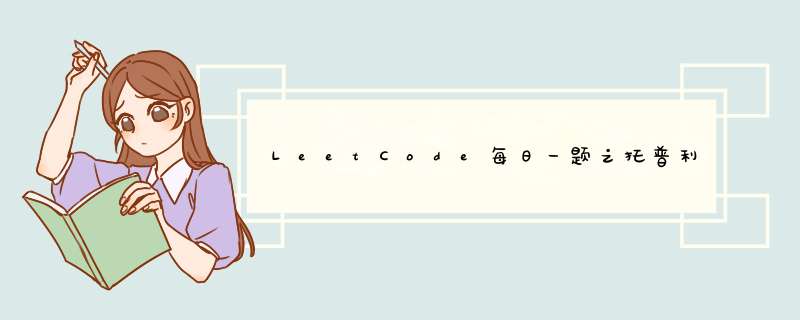
给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵，返回 true ；否则，返回 false 。

如果矩阵上每一条由左上到右下的对角线上的元素都相同，那么这个矩阵是 托普利茨矩阵 。

输入：matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
输出：true
解释：
在上述矩阵中, 其对角线为:
“[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”。
各条对角线上的所有元素均相同, 因此答案是 True 。

思路

暴力法解题：对于一开始就不知道思路的，先使用暴力法解决，问题解决了咱再考虑优化嘛
1、暴力法大致思路就是，写两个指针，再写两个循环，遍历一下就行

2、深度优先算法Java的实现：https://www.cnblogs.com/Huayra/p/10816415.html

方法一：(暴力遍历法)

class Solution {
    public boolean isToeplitzMatrix(int[][] matrix) {
    
    int m =matrix.length;
    int n =matrix[0].length;
    for(int i =0;i< m-1;i++){
        for(int j=0;j 
方法二：(深度优先算法) 
class Solution {

private boolean dfs(int[][] matrix ,int i,int j ,int value){
    //value ,预期值
        if( i>= matrix.length || j>=matrix[0].length) 
        return true; 
        //边界判断
        if(matrix[i][j] != value) 
        return false;
        
        return dfs(matrix ,i+1 ,j+1 ,value);
    }

public boolean isToeplitzMatrix(int[][] matrix) {
        int m =matrix.length , n =matrix[0].length;
        for(int i=0 ;i 
执行通过截图 
法一： 
 
法二： 
					
										


					

						
欢迎分享，转载请注明来源：内存溢出
原文地址: http://outofmemory.cn/zaji/5434544.html