Python-Matplotlib：查找线图的交集

Python-Matplotlib：查找线图的交集

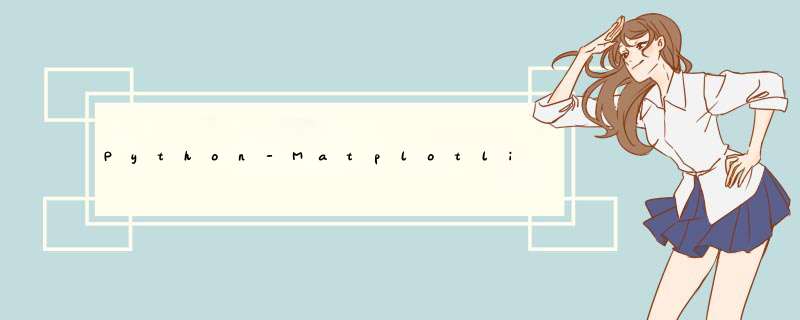
我们可以

scipy.interpolate.PiecewisePolynomial

用来创建由分段线性数据定义的函数。

p1=interpolate.PiecewisePolynomial(x1,y1[:,np.newaxis])p2=interpolate.PiecewisePolynomial(x2,y2[:,np.newaxis])

然后，我们可以利用这两个功能的区别，

def pdiff(x):    return p1(x)-p2(x)

并使用optimize.fsolve查找以下内容的根

pdiff

：

import scipy.interpolate as interpolateimport scipy.optimize as optimizeimport numpy as npx1=np.array([1.4,2.1,3,5.9,8,9,23])y1=np.array([2.3,3.1,1,3.9,8,9,11])x2=np.array([1,2,3,4,6,8,9])y2=np.array([4,12,7,1,6.3,8.5,12])p1=interpolate.PiecewisePolynomial(x1,y1[:,np.newaxis])p2=interpolate.PiecewisePolynomial(x2,y2[:,np.newaxis])def pdiff(x):    return p1(x)-p2(x)xs=np.r_[x1,x2]xs.sort()x_min=xs.min()x_max=xs.max()x_mid=xs[:-1]+np.diff(xs)/2roots=set()for val in x_mid:    root,infodict,ier,mesg = optimize.fsolve(pdiff,val,full_output=True)    # ier==1 indicates a root has been found    if ier==1 and x_min<root<x_max:        roots.add(root[0])roots=list(roots)        print(np.column_stack((roots,p1(roots),p2(roots))))

产量

[[ 3.85714286  1.85714286  1.85714286] [ 4.60606061  2.60606061  2.60606061]]

第一列是x值，第二列是在处评估的第一个PiecewisePolynomial的y值，

x

第三列是第二个PiecewisePolynomial的y值。