什么是线性表出？

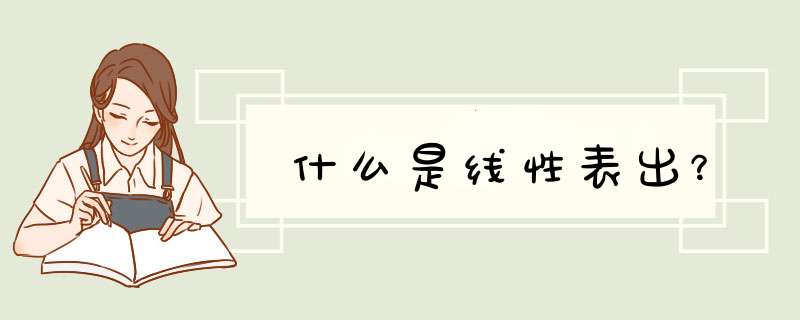
线性组合是线性代数的基本概念之一，设α₁，α₂，αₑ（e≥1)是域P上线性空间V中的有限个向量。

若干个同维数的行向量（或同维数的列向量）所组成的集合叫做向量组。

简介

卷积（Convolution)既是一个由含参变量的无穷积分定义的函数，又代表一种运算。其运算性质在线性系统理论、光学成像理论和傅里叶变换及其应用中经常用到。

卷积的运算性质有线性特性，复函数的卷积，可分离变量，卷积符合交换律，卷积符合结合律，坐标缩放性质，卷积位移不变性。

你把线性相关和线性表出的概念弄混了。我用比较通俗的概念给你理一下吧：

所谓线性相关，就是说这一堆向量里面“有没有用的向量”，比如我有了表示横纵坐标的向量（1,0）和（0,1）了，那么，在二维坐标系里面再给我一个（1,1），其实就没有必要了，这个时候，这三个向量是线性相关的。你把他延伸到方程组和向量的秩两个概念上就可以把线代串起来了，在方程组里面就相当于给了一个多于的方程，例如，给了x+y=1和2x+2y=2；在向量的秩里面，很显然如果把（1,0），（0,1），（1，1）组成一个矩阵算他们的秩应该是为2的，小于向量数目3。这就是线性相关了。

所谓线性表出，就是说，我现在这堆已有的向量组a1，a2……所构成的坐标系可以把你给出的这个向量b在坐标系中表示出来。因为你这个向量b可以被我这个坐标系表示，所以如果把该向量加入这个向量组中是一个没用的向量，所以合并后的向量组a1，a2,……b是线性相关的，所以R（a1，a2,……）=R（a1，a2……b）。但是不能表明a1，a2……这个向量组是否线性相关，由于条件不足。

回到你所给的题目，题目条件中a1，a2……am可以线性表示b而a1，a2……am-1不可以线性表示b，说明什么呢？说明，在b中有一维肯定不能用a1，a2……am-1表示，而可以用am表示。但是能否断定a1，a2……am-1和a1，a2……am的线性相关性呢？不能。因为条件不够我们推断出其相关性。

线性相关：若向量组满足k1a1+k2a2+...+knan

=

0,则必存在一组不全为0的数ki（i

=

0,1,...n）使之成立。

线性无关：向量组满足k1a1+k2a2+...+knan

=

0时，k1

=

k2

=

...

=

kn

=

0（必全为0）。

线性表出：a

=

k1a1+...+knan(k1..kn不全为0)

也就是说

一个向量可以由其他向量表达出来就是线性表出。

秩：一个向量组中极大线性无关向量组的个数等于该向量组的秩。

秩数只是表面一个向量组中的极大无关组的个数。

非要说

线性相关，线性无关，线性表出，向量组an与秩ra有什么关系

的话

联系只是间接地，不是那么显而易见。

比如

如果n个向量线性相关，那么该向量组的秩数一定小于n。

如果n个向量线性无关，那么该向量组的秩数等于n。

如果向量a可由n个向量组成的线性无关的向量组

i

线性表出

，那么将a添到向量组i中，此时该向量组的秩还是n。

希望对你有帮助，望采纳。

---