使用python,pytorch求海森Hessian矩阵

使用python,pytorch求海森Hessian矩阵

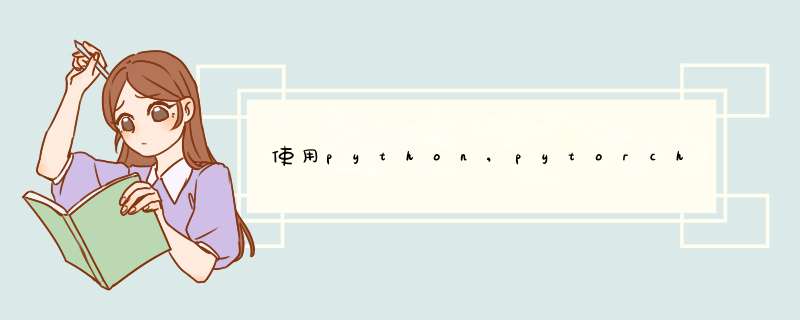
　　考虑一个函数$y=f(\textbf{x}) (R^n\rightarrow R)$，y的Hessian矩阵定义如下：

　　考虑一个函数:$$f(x)=b^Tx+\frac{1}{2}x^{T}Ax\\其中b^T=[1,3,5], A在代码中可读，可以自定义$$

　　求该函数在x = [0,0,0]处海森矩阵值的python代码如下：

　　本代码需要用到torch.autograd包中的核心函数torch.autograd.grad。

相邻随笔中有详细参考解析。

大致原理是人工求导并保留了计算图，所以求二阶导很方便。

如果想求解析形式的海森矩阵或许matlab中有相关的包能实现。

import torch

# 定义函数

x = torch.tensor([0., 0, 0], requires_grad=True)

b = torch.tensor([1., 3, 5])

A = torch.tensor([[-5, -3, -0.5], [-3, -2, 0], [-0.5, 0, -0.5]])

y = b@x + 0.5*x@A@x

# 计算一阶导数,因为我们需要继续计算二阶导数,所以创建并保留计算图

grad = torch.autograd.grad(y, x, retain_graph=True, create_graph=True)

# 定义Print数组,为输出和进一步利用Hessian矩阵作准备

Print = torch.tensor([])

for anygrad in grad[0]:  # torch.autograd.grad返回的是元组

    Print = torch.cat((Print, torch.autograd.grad(anygrad, x, retain_graph=True)[0]))

print(Print.view(x.size()[0], -1))

　　输出结果如下：