c 语言知识清单

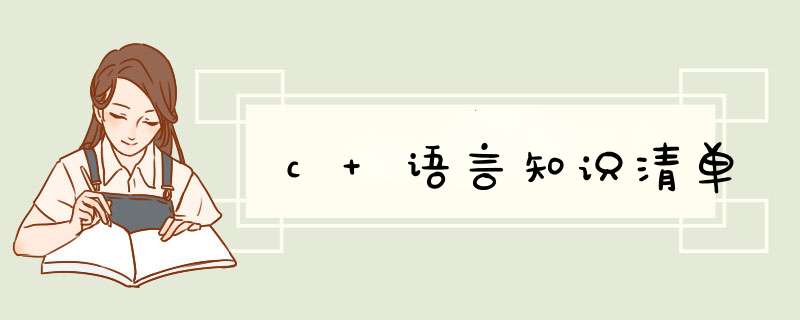
11 基本数据结构

1 数组

2 链表，双向链表

3 队列，单调队列，双端队列

4 栈，单调栈

12 中级数据结构

1 堆

2 并查集与带权并查集

3 hash 表

自然溢出

双hash

13 高级数据结构

1 树状数组

2 线段树，线段树合并

3 平衡树

Treap 随机平衡二叉树

Splay 伸展树

Scapegoat Tree 替罪羊树

4 块状数组，块状链表

5 树套树

线段树套线段树

线段树套平衡树

平衡树套线段树

6可并堆

左偏树

配对堆

7 KDtree，四分树

14 可持久化数据结构

1 可持久化线段树

主席树

2 可持久化平衡树

3 可持久化块状数组

15 字符串相关算法及数据结构

1 KMP

2 AC 自动机

3 后缀数组

4 后缀树

5 后缀自动机

6 字典树 Trie

7 manacher

16 图论相关

1 最小生成树

prim

kruskal

2 最短路，次短路，K短路

spfa

dijkstra

floyd

3 图的连通

连通分量

割点，割边

4 网络流

最大流

最小割

费用流

分数规划

5 树相关

树上倍增，公共祖先

树链剖分

树的分治算法（点分治，边分治，动态？树分治）

动态树 （LCT，树分块）

虚树

prufer编码

7 拓扑排序

8 欧拉图

9 二分图

KM算法

匈牙利算法

17 数学相关

1 （扩展）欧几里得算法，筛法，快速幂

斐蜀定理

更相减损术

2 欧拉函数与降幂大法

3 费马小定理

4 排列组合

lucas定理

5 乘法逆元

6 矩阵乘法

7 数学期望与概率

8 博弈论

sg函数

树上删边游戏

9 拉格朗日乘子法

10 中国剩余定理

11 线性规划与网络流

12 单纯型线性规划

13 辛普森积分

14 模线性方程组

15 容斥原理与莫比乌斯反演

16 置换群

17 快速傅里叶变换

18 大步小步法（BSGS），扩展BSGS

18 动态规划

1 一般，背包，状压，区间，环形，树形，数位动态规划

记忆化搜索

斯坦纳树

背包九讲

2 斜率优化与 四边形不等式优化

3 环 + 外向树上的动态规划

4 插头动态规划

19 计算几何

1 计算几何基础

2 三维计算几何初步

3 梯形剖分与三角形剖分

4 旋转卡壳

5 半平面交

6 pick定理

7 扫描线

110 搜索相关

1 bfs，dfs

2 A 算法

3 迭代加深搜索，双向广搜

111 特殊算法

1 莫队算法，树上莫队

2 模拟退火

3 爬山算法

4 随机增量法

112 其它重要工具与方法

1模拟与贪心

2 二分，三分法（求偏导）

3 分治，CDQ分治

4 高精度

5 离线

6 ST表

113 STL

1 map

2 priority_queue

3 set

4 bitset

5 rope

114 非常见算法

1 朱刘算法

2 弦图与区间图

其实以上的算法能学完1/3就已经很好了

望采纳，谢谢

要做傅立叶变换，一般用快速傅立叶变换。这个前面已经有人说过了。

不过不必自己写，有音频处理的库：

bass

>

何编程语言是难学的,真正的工作中有时候学习一个新语法只有不到一周的时间,语法而言都一样,如果还停留在语法层学习的上面,编写程序的道路你就连门都没有入

但是后续的 数据结构和算法 稍微要看下书了,开始接触算法了,着和语法没有关系,之所以要先学好语法是为了能看懂用语法描叙的算法,学通了用任何语言来描叙都一样,到了这个阶段的就相当于抬起一条腿准备跨到起跑线一样,但还是没有入门

到编译原理 和 图灵机 再到 自己编写微型的 *** 作系统 就需要有个老师来引导了

我学软件开发就是从C开始一路由 ->国家数据库3级-> 程序员->高级程序员->系统分析师考上去然后通过近9年的工作,体会是如果你能够在市面上或者学校里精确买到或者学到的一门知识往往就表示你的层次还是不能让你得兴应手的在行业中创造你能想像的东西,真正的解决问题需要很多本书再加上80%以上的自己创造和理解才能做出来的时候才算真正懂得了你的工作

一个程序员需要这样的经历

楼上的估计最高学历不过是理工科的一个大学生,应该还没毕业,没有在计算机行业呆过,在做芯片处理的工作中比如DSP芯片设计需要你天天接触算法,但是这和C语言本身有关系吗傅立叶算法是数学家傅立叶设计出来的数学模型但是不适合做在计算机软件里面(运算量太大了比如离散的傅立叶变换等同于用序列Y(n×1列矢量)乘以n×n矩阵Fn，需要n×n次乘法。若n=1024,则是104，8576次乘法运算。什么概念呢？如果你选用的CPU单周期指令为25ns, 单周期也可以完成一次乘法运算，那么要计算1024点的傅立叶变换则需要262144ms,这还不包括加法或其它运算),我给出C算法如下:

void kkfft(double pr[], double pi[], int n, int k, double fr[], double fi[], int l, int il)

{

int it,m,is,i,j,nv,l0;

double p,q,s,vr,vi,poddr,poddi;

for (it=0; it<=n-1; it++)

{

m = it;

is = 0;

for(i=0; i<=k-1; i++)

{

j = m/2;

is = 2is+(m-2j);

m = j;

}

fr[it] = pr[is];

fi[it] = pi[is];

}

//----------------------------

pr[0] = 10;

pi[0] = 00;

p = 6283185306/(10n);

pr[1] = cos(p);

pi[1] = -sin(p);

if (l!=0)

pi[1]=-pi[1];

for (i=2; i<=n-1; i++)

{

p = pr[i-1]pr[1];

q = pi[i-1]pi[1];

s = (pr[i-1]+pi[i-1])(pr[1]+pi[1]);

pr[i] = p-q;

pi[i] = s-p-q;

}

for (it=0; it<=n-2; it=it+2)

{

vr = fr[it];

vi = fi[it];

fr[it] = vr+fr[it+1];

fi[it] = vi+fi[it+1];

fr[it+1] = vr-fr[it+1];

fi[it+1] = vi-fi[it+1];

}

m = n/2;

nv = 2;

for (l0=k-2; l0>=0; l0--)

{

m = m/2;

nv = 2nv;

for(it=0; it<=(m-1)nv; it=it+nv)

for (j=0; j<=(nv/2)-1; j++)

{

p = pr[mj]fr[it+j+nv/2];

q = pi[mj]fi[it+j+nv/2];

s = pr[mj]+pi[mj];

s = s(fr[it+j+nv/2]+fi[it+j+nv/2]);

poddr = p-q;

poddi = s-p-q;

fr[it+j+nv/2] = fr[it+j]-poddr;

fi[it+j+nv/2] = fi[it+j]-poddi;

fr[it+j] = fr[it+j]+poddr;

fi[it+j] = fi[it+j]+poddi;

}

}

if(l!=0)

for(i=0; i<=n-1; i++)

{

fr[i] = fr[i]/(10n);

fi[i] = fi[i]/(10n);

}

if(il!=0)

for(i=0; i<=n-1; i++)

{

pr[i] = sqrt(fr[i]fr[i]+fi[i]fi[i]);

if(fabs(fr[i])<0000001fabs(fi[i]))

{

if ((fi[i]fr[i])>0)

pi[i] = 900;

else

pi[i] = -900;

}

else

pi[i] = atan(fi[i]/fr[i])3600/6283185306;

}

return;

}

另外,虚机团上产品团购,超级便宜

实现(C描述)

#include <stdioh>

#include <mathh>

#include <stdlibh>

//#include "complexh"

// --------------------------------------------------------------------------

#define N 8 //64

#define M 3 //6 //2^m=N

#define PI 31415926

// --------------------------------------------------------------------------

float twiddle[N/2] = {10, 0707, 00, -0707};

float x_r[N] = {1, 1, 1, 1, 0, 0, 0, 0};

float x_i[N]; //N=8

/

float twiddle[N/2] = {1, 09951, 09808, 09570, 09239, 08820, 08317, 07733,

07075, 06349, 05561, 04721, 03835, 02912, 01961, 00991,

00000,-00991,-01961,-02912,-03835,-04721,-05561,-06349,

-07075,-07733, 08317,-08820,-09239,-09570,-09808,-09951}; //N=64

float x_r[N]={1,1,1,1,1,1,1,1,

1,1,1,1,1,1,1,1,

1,1,1,1,1,1,1,1,

1,1,1,1,1,1,1,1,

0,0,0,0,0,0,0,0,

0,0,0,0,0,0,0,0,

0,0,0,0,0,0,0,0,

0,0,0,0,0,0,0,0,};

float x_i[N];

/

FILE fp;

// ----------------------------------- func -----------------------------------

/

初始化输出虚部

/

static void fft_init( void )

{

int i;

for(i=0; i<N; i++) x_i[i] = 00;

}

/

反转算法将时域信号重新排序

这个算法有改进的空间

/

static void bitrev( void )

{

int p=1, q, i;

int bit_rev[ N ]; //

float xx_r[ N ]; //

bit_rev[ 0 ] = 0;

while( p < N )

{

for(q=0; q<p; q++)

{

bit_rev[ q ] = bit_rev[ q ] 2;

bit_rev[ q + p ] = bit_rev[ q ] + 1;

}

p = 2;

}

for(i=0; i<N; i++) xx_r[ i ] = x_r[ i ];

for(i=0; i<N; i++) x_r[i] = xx_r[ bit_rev[i] ];

}

/ ------------ add by sshc625 ------------ /

static void bitrev2( void )

{

return ;

}

/ /

void display( void )

{

printf("\n\n");

int i;

for(i=0; i<N; i++)

printf("%f\t%f\n", x_r[i], x_i[i]);

}

/

/

void fft1( void )

{ fp = fopen("log1txt", "a+");

int L, i, b, j, p, k, tx1, tx2;

float TR, TI, temp; // 临时变量

float tw1, tw2;

/ 深M 对层进行循环 L为当前层, 总层数为M /

for(L=1; L<=M; L++)

{

fprintf(fp,"----------Layer=%d----------\n", L);

/ b的意义非常重大,b表示当前层的颗粒具有的输入样本点数 /

b = 1;

i = L - 1;

while(i > 0)

{

b = 2;

i--;

}

// -------------- 是否外层对颗粒循环, 内层对样本点循环逻辑性更强一些呢! --------------

/

outter对参与DFT的样本点进行循环

L=1, 循环了1次(4个颗粒, 每个颗粒2个样本点)

L=2, 循环了2次(2个颗粒, 每个颗粒4个样本点)

L=3, 循环了4次(1个颗粒, 每个颗粒8个样本点)

/

for(j=0; j<b; j++)

{

/ 求旋转因子tw1 /

p = 1;

i = M - L; // M是为总层数, L为当前层

while(i > 0)

{

p = p2;

i--;

}

p = p j;

tx1 = p % N;

tx2 = tx1 + 3N/4;

tx2 = tx2 % N;

// tw1是cos部分, 实部; tw2是sin部分, 虚数部分

tw1 = ( tx1>=N/2) -twiddle[tx1-N/2] : twiddle[ tx1 ];

tw2 = ( tx2>=N/2) -twiddle[tx2-(N/2)] : twiddle[tx2];

/

inner对颗粒进行循环

L=1, 循环了4次(4个颗粒, 每个颗粒2个输入)

L=2, 循环了2次(2个颗粒, 每个颗粒4个输入)

L=3, 循环了1次(1个颗粒, 每个颗粒8个输入)

/

for(k=j; k<N; k=k+2b)

{

TR = x_r[k]; // TR就是A, x_r[k+b]就是B

TI = x_i[k];

temp = x_r[k+b];

/

如果复习一下 (a+jb)(c+jd)两个复数相乘后的实部虚部分别是什么

就能理解为什么会如下运算了, 只有在L=1时候输入才是实数, 之后层的

输入都是复数, 为了让所有的层的输入都是复数, 我们只好让L=1时候的

输入虚部为0

x_i[k+b]tw2是两个虚数相乘

/

fprintf(fp, "tw1=%f, tw2=%f\n", tw1, tw2);

x_r[k] = TR + x_r[k+b]tw1 + x_i[k+b]tw2;

x_i[k] = TI - x_r[k+b]tw2 + x_i[k+b]tw1;

x_r[k+b] = TR - x_r[k+b]tw1 - x_i[k+b]tw2;

x_i[k+b] = TI + temptw2 - x_i[k+b]tw1;

fprintf(fp, "k=%d, x_r[k]=%f, x_i[k]=%f\n", k, x_r[k], x_i[k]);

fprintf(fp, "k=%d, x_r[k]=%f, x_i[k]=%f\n", k+b, x_r[k+b], x_i[k+b]);

} //

} //

} //

}

/

------------ add by sshc625 ------------

该实现的流程为

for( Layer )

for( Granule )

for( Sample )

/

void fft2( void )

{ fp = fopen("log2txt", "a+");

int cur_layer, gr_num, i, k, p;

float tmp_real, tmp_imag, temp; // 临时变量, 记录实部

float tw1, tw2;// 旋转因子,tw1为旋转因子的实部cos部分, tw2为旋转因子的虚部sin部分

int step; // 步进

int sample_num; // 颗粒的样本总数(各层不同, 因为各层颗粒的输入不同)

/ 对层循环 /

for(cur_layer=1; cur_layer<=M; cur_layer++)

{

/ 求当前层拥有多少个颗粒(gr_num) /

gr_num = 1;

i = M - cur_layer;

while(i > 0)

{

i--;

gr_num = 2;

}

/ 每个颗粒的输入样本数N' /

sample_num = (int)pow(2, cur_layer);

/ 步进 步进是N'/2 /

step = sample_num/2;

/ /

k = 0;

/ 对颗粒进行循环 /

for(i=0; i<gr_num; i++)

{

/

对样本点进行循环, 注意上限和步进

/

for(p=0; p<sample_num/2; p++)

{

// 旋转因子, 需要优化

tw1 = cos(2PIp/pow(2, cur_layer));

tw2 = -sin(2PIp/pow(2, cur_layer));

tmp_real = x_r[k+p];

tmp_imag = x_i[k+p];

temp = x_r[k+p+step];

/(tw1+jtw2)(x_r[k]+jx_i[k])

real : tw1x_r[k] - tw2x_i[k]

imag : tw1x_i[k] + tw2x_r[k]

我想不抽象出一个

typedef struct {

double real; // 实部

double imag; // 虚部

} complex; 以及针对complex的 *** 作

来简化复数运算是否是因为效率上的考虑!

/

/ 蝶形算法 /

x_r[k+p] = tmp_real + ( tw1x_r[k+p+step] - tw2x_i[k+p+step] );

x_i[k+p] = tmp_imag + ( tw2x_r[k+p+step] + tw1x_i[k+p+step] );

/ X[k] = A(k)+WB(k)

X[k+N/2] = A(k)-WB(k) 的性质可以优化这里/

// 旋转因子, 需要优化

tw1 = cos(2PI(p+step)/pow(2, cur_layer));

tw2 = -sin(2PI(p+step)/pow(2, cur_layer));

x_r[k+p+step] = tmp_real + ( tw1temp - tw2x_i[k+p+step] );

x_i[k+p+step] = tmp_imag + ( tw2temp + tw1x_i[k+p+step] );

printf("k=%d, x_r[k]=%f, x_i[k]=%f\n", k+p, x_r[k+p], x_i[k+p]);

printf("k=%d, x_r[k]=%f, x_i[k]=%f\n", k+p+step, x_r[k+p+step], x_i[k+p+step]);

}

/ 开跳!:) /

k += 2step;

}

}

}

/

后记:

究竟是颗粒在外层循环还是样本输入在外层, 好象也差不多, 复杂度完全一样

但以我资质愚钝花费了不少时间才弄明白这数十行代码

从中我发现一个于我非常有帮助的教训, 很久以前我写过一部分算法, 其中绝大多数都是递归

将数据量减少, 减少再减少, 用归纳的方式来找出数据量加大代码的规律

比如FFT

1 先写死LayerI的代码; 然后再把LayerI的输出作为LayerII的输入, 又写死代码;

大约3层就可以统计出规律来 这和递归也是一样, 先写死一两层, 自然就出来了!

2 有的功能可以写伪代码, 不急于求出结果, 降低复杂性, 把逻辑结果定出来后再添加

比如旋转因子就可以写死, 就写10 流程出来后再写旋转因子

寥寥数语, 我可真是流了不少汗! Happy!

/

void dft( void )

{

int i, n, k, tx1, tx2;

float tw1,tw2;

float xx_r[N],xx_i[N];

/

clear any data in Real and Imaginary result arrays prior to DFT

/

for(k=0; k<=N-1; k++)

xx_r[k] = xx_i[k] = x_i[k] = 00;

// caculate the DFT

for(k=0; k<=(N-1); k++)

{

for(n=0; n<=(N-1); n++)

{

tx1 = (nk);

tx2 = tx1+(3N)/4;

tx1 = tx1%(N);

tx2 = tx2%(N);

if(tx1 >= (N/2))

tw1 = -twiddle[tx1-(N/2)];

else

tw1 = twiddle[tx1];

if(tx2 >= (N/2))

tw2 = -twiddle[tx2-(N/2)];

else

tw2 = twiddle[tx2];

xx_r[k] = xx_r[k]+x_r[n]tw1;

xx_i[k] = xx_i[k]+x_r[n]tw2;

}

xx_i[k] = -xx_i[k];

}

// display

for(i=0; i<N; i++)

printf("%f\t%f\n", xx_r[i], xx_i[i]);

}

// ---------------------------------------------------------------------------

int main( void )

{

fft_init( );

bitrev( );

// bitrev2( );

//fft1( );

fft2( );

display( );

system( "pause" );

// dft();

return 1;

}

本文来自CSDN博客，转载请标明出处：>

内存用的太猛了，不够了。

办法：1，放外存里

2，选个大内存的CPU

3、用ARM芯片，它可以接N兆的内存

4、用DSP或专用协处理器来处理傅立叶变换

5、你就不应该用软件来处理，效率很差的。

以上就是关于c 语言知识清单全部的内容，包括:c 语言知识清单、怎样用vc或c语言编写输出MP3频谱的程序、DSP实验 让我用C语言编写程序完成计算sin(2.3π)+cos(1.7π)的值等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！