matlab 中regress()怎么用

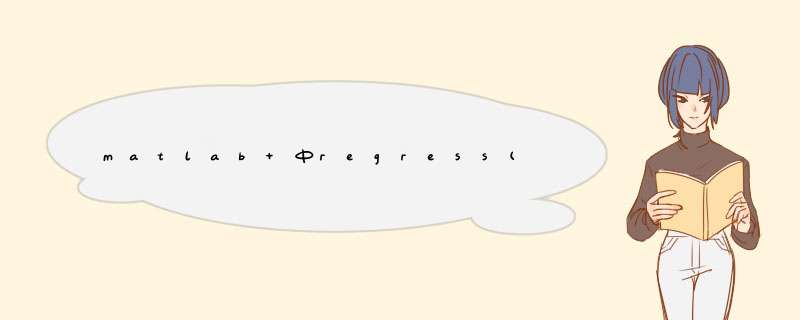
[b,bint,r,rint,stats] = regress(y,x,alpha) bookiLoveMatlabcn

%y 多元拟合的变量值的向量

%x 多元拟合的自变量的值的矩阵

%alpha 显著性水平，缺省的时候为005

%b 回归得到的自变量系数

%bint b的95%的置信区间矩阵

%r 残差向量

%rint 区间矩阵。

试试吧

对应幂指数函数的拟合，通过指数转换，就可以直接使用regress多元线性回归函数，求得其斜率k。最后用plot绘图函数绘出该函数的图形，其实现方法：

%数据

w=[56,62,69,77,94,105];

y=[305,327,358,380,418,436];

x=w^(2/3);

%斜率

k=regress(y',x')

%绘图

w1=56:105;y1=kw^(2/3);

plot(w,y,'',w1,y1,'r-')

运行上述代码，可得到如下结果及图形。

主要是用regress函数来进行：给你举个例子来说明吧。

x=[0 1 2 3 4 ]';y=[10 13 15,20 23]';

x=[ones(5,1),x]; %给出两个数组元素

[b,bint,r,rint,stats]=regress(y,x,005); ％对x和y进行一元线性回归，并得到相关系数，其中，stats中第一个数即为相关系数，大于09就认为拟合很好。

结果：stats =

09829 1719474 00010 00063

即为09829

当然可以按你所说的求解，关键是看你建立的回归模型的意义。还有，从回归原理看，一般认为回归方程要有常数项，这样才能保证回归的有效性。比如，如果没有 ones(4,1) 这一列，matlab会提示： R-square and the F statistic are not well-defined unless X has a column of ones也就是没有ones(4,1)，模型的有效性将会被质疑。

首先，把给出的向量方程，改写为

a1X+a2Y+a3=-(X²+Y²)

Z(x,y)=-(x²+y²)=a1x+a2y+a3

然后，我们用regress最小二乘法回归函数来拟合a1、a2、a3的系数

x=[。。。] %数据

y=[。。。] %数据

Z=-(x²+y²);

X=[x  y  ones(n,1)]; %n=x或y数据的个数

a= regress(Z,X); %求出系数a1,a2和a3

此时，我们就可以得到如下系数：

a1=a(1),a2=a(2)和a3=a(3)

调用regress函数就能直接求出拟合度。

[B,BINT,R,RINT,STATS]

=

REGRESS(y,X,alpha)

uses

the

input,

ALPHA

alpha为显著性水平(缺省005)

,b,bint

为回归系数估计值和它们的置信区间，r,rint

为残差（向量）及其置信区间，stats

是用于检验回归模型的统

计量，有四个数值，第一个是R^2

，也就是拟合度的平方，第二个是F，第三个是与F

对应的概率

p，

α

<

p

拒绝

H0，回归模型成立，

第四个是残差的方差s^2

。残差及其置信区间可以用

rcoplot(r,rint)画图。

clear;

clc;

x = [50 100 150 200 250 300 350 400 450 500];

y = [40 80 120 160 200];

[myx,myy] = meshgrid(x,y);

z = [005 005 005 005 005

025 015 011 005 005

05 02 02 004 004

16 1 05 011 007

25 24 114 034 012

32 27 154 07 021

34 31 21 115 03

375 35 256 14 06

4 38 295 2 09

42 4 32 22 11];

cxd_1 = reshape(myx',50,1);

cxd_2 = reshape(myy',50,1);

cxd_3 = ones(50,1);

cxd_X = [cxd_1 cxd_2 cxd_3];

cxd_Y = z(:);

myb = regress(cxd_Y,cxd_X);

a = myb(1)

b = myb(2)

c = myb(3)

结果：

a =

00072

b =

-00132

c =

10057

copyright (c) by cxd1301

以上就是关于matlab 中regress()怎么用全部的内容，包括:matlab 中regress()怎么用、线性最小二乘法的程序、一元线性回归模型的拟合优度检验的matlab代码等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！