cosx^2的不定积分

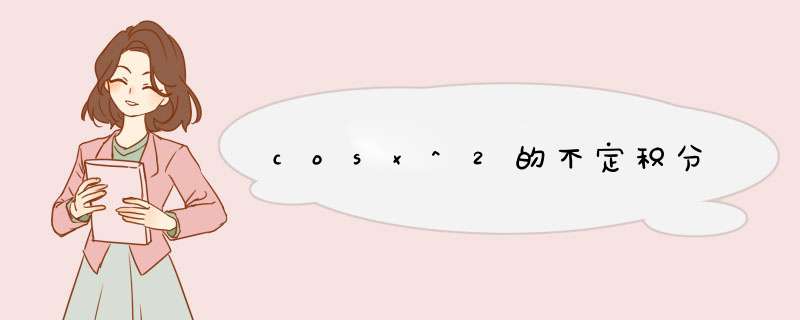
∫ cos²x dx=(1/2)∫ (1+cos2x) dx=(1/2)x + (1/4)sin2x + C。解题过程：解：原式=1/2∫(1+cos2x)dx=1/2∫1dx+1/2∫cos2xdx=1/2x+1/4∫cos2xdx=(1/2)x + (1/4)sin2x + C。

扩展资料：

求函数f(x)的不定积分，就是要求出f(x)的所有的原函数，由原函数的性质可知，只要求出函数f(x)的一个原函数，再加上任意的常数C就得到函数f(x)的不定积分。

不定积分的公式：

1、∫ a dx = ax + C，a和C都是常数

2、∫ x^a dx = [x^(a + 1)]/(a + 1) + C，其中a为常数且 a ≠ -1

3、∫ 1/x dx = ln|x| + C

4、∫ a^x dx = (1/lna)a^x + C，其中a u003e 0 且 a ≠ 1

5、∫ e^x dx = e^x + C