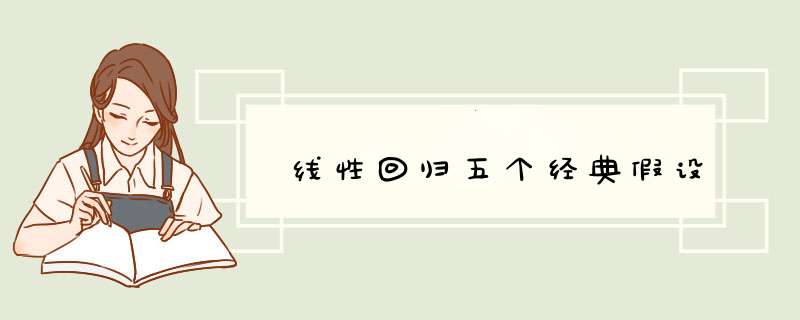
线性回归五个经典假设

线性回归五个经典假设：1、随机误差项是一个期望值或平均值为0的随机变量；2、对于解释变量的所有观测值，随机误差项有相同的方差；3、随机误差项服从正态分布；4、解释变量是确定性变量，不是随机变量，与随机误差项彼此之间相互独立；5、解释变量之间不存在精确的线性关系，即解释变量的样本观测值矩阵是满秩矩阵。

扩展资料：

线性回归方程是利用数理统计中的回归分析，来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一。线性回归也是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。按自变量个数可分为一元线性回归分析方程和多元线性回归分析方程。

线性回归有很多实际用途。分为以下两大类：

1 如果目标是预测或者映射，线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。当完成这样一个模型以后，对于一个新增的X值，在没有给定与它相配对的y的情况下，可以用这个拟合过的模型预测出一个y值。

2 给定一个变量y和一些变量X1,...,Xp，这些变量有可能与y相关，线性回归分析可以用来量化y与Xj之间相关性的强度，评估出与y不相关的Xj，并识别出哪些Xj的子集包含了关于y的冗余信息。