基于FPGA的WALLACE TREE乘法器设计

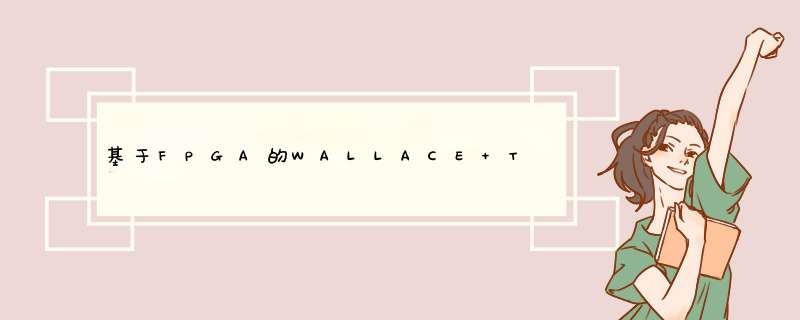
　　本文着重介绍了一种基于WALLACETREE优化算法的改进型乘法器架构。根据FPGA内部标准独特slice单元，有必要对WALLACE TREE部分单元加以研究优化，从而让在FPGA的乘法器设计中的关键路径时延得以减小，整体时钟性能得以提高。也能够使FPGA的面积资源合理优化，提高器件的整体资源利用率。

　　1 WALLACE TREE结构

　　WALLACE TREE是对部分积规约，减小乘法器关键路径时延的一种算法。传统WALLACE TREE结构的CSA(Carry Save Adder)阵列乘法器如图1所示，其中“·”代表生成的多个部分乘积项，相应电路中用逻辑与门来实现。求和阵列将前面生成的多个部分积通过3：2 CSA压缩器，将其压缩成2个部分积，最后通过末级进位相加得到所需的最终乘积结果。图中矩形框所示为3：2 CSA压缩器，其电路逻辑等效于一个全加器结构。通过运算可知N个部分积，要经类似的log(2N/3)级3：2压缩，就可得到2个部分积。

　　2 压缩器的优化

　　由于FPGA内部的结构是固定的，没有以上WALLACE TREE所需要的CSA标准全加器结构。因此，在传统的FPGA电路综合实现时，该CSA全加

　　器被综合在FPGA内部查找表(LUT)和进位链中，占用了整个slice单元的资源。由于经典WALLACETREE结构不具有良好的对称性且需要权重对齐等因素，势必要增大FPGA电路的复杂度，增加大量的FPGA内部布局和布线资源，在FPGA中不规则的布局布线结构，也增大了关键路径的时延。

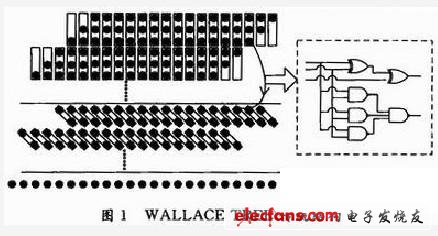
　　为在FPGA中较好地实现WALLACE TREE结构，结合FPGA中最小标准单元的结构silce，对CSA全加器单元结构加以改进。如图2所示，可将WALLACE TREE相邻的平级3：2 CSA压缩器合并成一个6：4压缩器。该压缩器只需使用1个FPGA的silce资源，就能实现其数字逻辑。下面以3×3乘法器为例，进行WALLACE TREE压缩器的推导和优化。如图2的第一个部分积，部分积低位空白应补0，高位空白位用该部分积的最高位补齐。

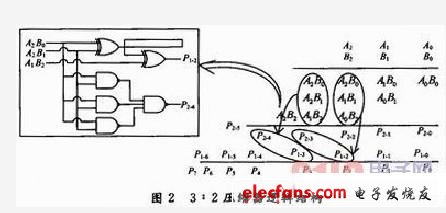
　　下面对2个3：2 CSA压缩器合并成一个6：4压缩器单元运算逻辑做理论推导，其中：

　　合并这两项3：2压缩为6：4压缩时，A1B2和P23属同级进位，在计算过程中可将这两项的位置互换，因此上式可推导演化成：