基于FPGA的神经网络算法的设计

随着4C 技术的迅猛发展，以及近十多年来智能控制技术的成就，智能控制在工业用仪器仪表和信息电器（ IA）产业中得到了广泛应用，其实现手段也趋于多样化。采用FPGA 实现控制器与使用冯·诺伊曼（VonNeumann）结构的微控制器（MCU）相比，具有信息流并行性、快速性、灵活性和易于扩展等特点。特别在实现复杂智能控制策略时，由于微控制器只能顺序执行程序，随着算法复杂程度的提高，执行速度必将受到限制。FPGA 可固件串行与并行实现算法，从本质上提高了处理速度，对实时性要求较高的智能控制过程来说是一种有效的实现途径。

随着FPGA技术的不断发展，各种智能控制策略的FPGA 固核实现的研究随之活跃。Henriette Ossoing等人完成了神经网络的FPGA 实现并应用于监控和诊断系统中[1] ,Cirstea Marcian 等人将基于FPGA 的神经网络控制器用于驱动电机。在第二次数字浪潮涌现之际，FPGA 的灵活可编程性等特点非常适合具有生命周期短、批量大的数字消费类电子产品的研制开发。

单神经元PID 控制器是一种具有自学习能力和自适应能力的良好控制器， 它不但结构简单、学习算法物理意义明确、计算量小，参数调整容易，且能适应环境变化，具有较强的鲁棒性，比较适合实际使用。仍是实际工业过程中广泛采用的一种比较有效的控制方法。但当被控对象存在非线性和时变特性时，传统的PID 控制器往往难以获得满意的控制效果。神经网络以其强大的信息综合能力为解决复杂控制系统问题提供了理论基础，许多学者也通过软件仿真的形式验证了神经网络控制的可行性并提出了一些新的算法，但由于目前没有相应的硬件支持，只通过软件编程，利用串行方法来实现神经网络控制必然导致运算速度低，难以保证实时控制。而正如前文锁说的FPGA结构灵活、通用性强、速度快、功耗低，用它来构造神经网络，可以灵活地实现各种运算功能和学习规则，并且设计周期短、系统速度快、可靠性高。足以弥补PID控制器出现的各种问题。

本文主要介绍了用FPGA实现单神经元自适应PID控制器的方法，并对基于BP神经网络整定的PID控制器的FPGA设计做了概述。

神经元自适应PID控制器的基本原理和算法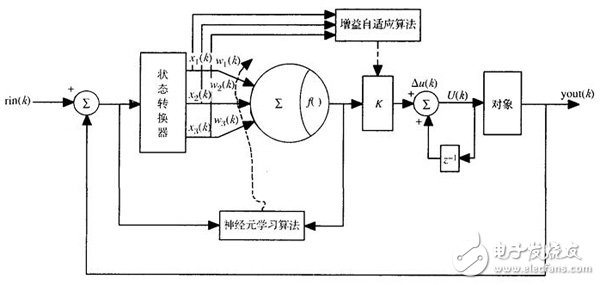

单神经元PID控制器的结构

三输入单神经元模型。其中x1，x2，x3是输入量，w1、w2、w3是对应的权值，K为比例系数。
与传统PID控制器经离散处理后的增量表达式
y（k）=kie（k）+kp（e（k）-e（k-1）+kd（e（k）-2e（k-1）+e（k-2））
比较而知，权值w1、w2、w3分别对应于传统PID控制器的ki，kp和kd。

学习算法
经过大量的实际应用，实践表明PID参数的在线学习修正主要与芿（k）和e（k）有关。因此可将单神经元自适应PID控制算法中的加权系数学习修正部分进行修改。

本文里用FPGA实现的单神经元学习算法就采用了这种基于改进规则的方法。

神经元算法在FPGA上的实现

FPGA上浮点数的运算

浮点加、减、乘、除运算单元的设计

神经元PID算法离不开浮点运算，浮点运算在高级语言中使用很方便，但是通过硬件来实现就比较复杂，所以大多数的EDA软件目前还不支持浮点运算，浮点运算器件只能自行设计，其中主要考虑的是运算精度、运算速度、资源占用以及设计复杂度。

浮点数的加法和减法需要经过对阶、尾数运算、规格化、舍入 *** 作和判断结果正确性5个步骤，整个运算过程由op_state状态机控制，op输入端决定运算法则（0为加法，1为减法），a、b两端分别输入24位浮点数格式的加数和被加数，经过float_add_minus模块的对阶、尾数加（减）、舍入 *** 作和判断结果正确性四步运算，再由result_ normalizaTIon模块规格化处理后输出。

浮点乘法相对比较简单，两个浮点数相乘，其乘积的阶码是两个数的阶码之和，乘积的尾数是两个数尾数的乘积，符号是相乘数符号的异或，结果一样需要规格化。

同理，浮点除法运算中，商的阶码是两个数的阶码之差（被除数减除数），商的尾数是两个数尾数的商，符号是两个数符号的异或，注意这里结果的规格化与以往不同，是向右规格化 *** 作。

在具体实现中，乘法器的尾数乘积运算采用了booth算法，除法器的尾数相除运算采用了移位相减的方法。

二进制与十进制浮点数相互转换电路的设计