sin z 的洛朗级数展开，在零点展开，要求详细点，别直接答案

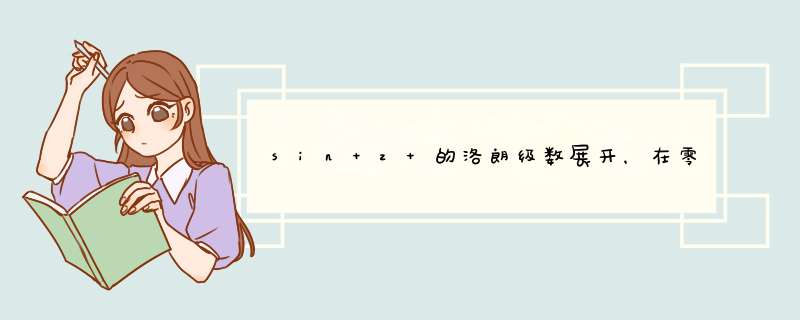
∵(sinz)'=cosz=sin(π/2+z)，(sinz)''=cos(π/2+z)=sin(2π/2+z)，……，sinz的n阶导函数(sinz)^(n)=sin(nπ/2+z)。

∴(sinz)^(n)丨(z=0)=0n=2m、=(-1)^mn=2m+1，其中，m=0,1,2，……，∞。

∴sinz=z-z³/(3!)+……+[(-1)^m][z^(2m+1)]/(2m+1)!+……。其中丨z丨<+∞。

供参考。

先看展成正弦级数，先把f（x）延拓到区间（1，2］，使得f（x）=2-x，x∈（1，2］

再把f（x）奇性延拓到区间［-2，0）上，使得f（x）=-f（-x），x∈［-2，0）

再把f（x）以周期为4延拓到整个实轴上去，令x=2t/π，记g（t）=f（x）=f（2t/π）

则g（t）是周期为2π的奇函数，所以an=0

bn=（∫（-π，π）g（t）sin（nt）dt）/π=（2/π）（∫（0，π）g（t）sin（nt）dt

最后再把f（x）以周期为2延拓到整个实轴上去，令x=t/π，记g（t）=f（x）=f（t/π）

则g（t）是周期为2π的偶函数，所以bn=0

an=（∫（-π，π）g（t）cos（nt）dt）/π=（2/π）（∫（0，π）g（t）cos（nt）dt

=1/2-4∑（cos（2n-1）πx）/［（2n-1）π］²，x∈［0，1］

正弦=股长/弦长：

勾股弦放到圆里。弦是圆周上两点连线。最大的弦是直径。 把直角三角形的弦放在直径上，股就是∠A所对的弦，即正弦，勾就是余下的弦——余弦。

按现代说法，正弦是直角三角形的对边与斜边之比。

现代正弦公式是：

sin = 直角三角形的对边比斜边。

斜边为r，对边为y，邻边为a。斜边r与邻边a夹角Ar的正弦sinA=y/r。

这个不行，正弦级数一定是奇函数，而cosx是偶函数，所以在理论上是做不到的

其实这个很好理解，正弦级数，也就是一系列正弦函数的和函数，而正弦函数是奇函数，所以n多个奇函数加起来还是奇函数。

同理，余弦级数一定是偶函数。

所以可以得出这样的结论：

在做傅里叶级数展开时，若原函数是奇函数，则展开后只有正弦项，也就是正弦级数（也就不用计算余弦项的系数，因为一定全为零）；若原函数是偶函数，则展开后只有余弦项，也就是余弦级数；若原函数为非奇非偶函数，则展开项中一定既有正弦项也有余弦项。

（注：这里常数项归为余弦项）

f(x)=(π-x)/2展开成正弦级数是2/π ∫(π-x/2)sinn2xdx。

=a0/2+∑ancosnωx+bnsinnωx

∑的n从1~∞T=π

ω=2π/T=2an=2/π ∫f(x)cosnωxdx n=0,1,2bn

=2/π ∫f(x)sinnωxdx n

=1,2,3an=2/π ∫(π-x/2)cosn2xdxbn

=2/π ∫(π-x/2)sinn2xdx

正弦函数

一般的，在直角坐标系中，给定单位圆，对任意角α，使角α的顶点与原点重合，始边与x轴非负半轴重合，终边与单位圆交于点P（u，v），那么点P的纵坐标v叫做角α的正弦函数，记作v=sinα。

通常，我们用x表示自变量，即x表示角的大小，用y表示函数值，这样我们就定义了任意角的三角函数y=sin x，它的定义域为全体实数，值域为[-1,1]。