回溯法--全排列

概述全排列

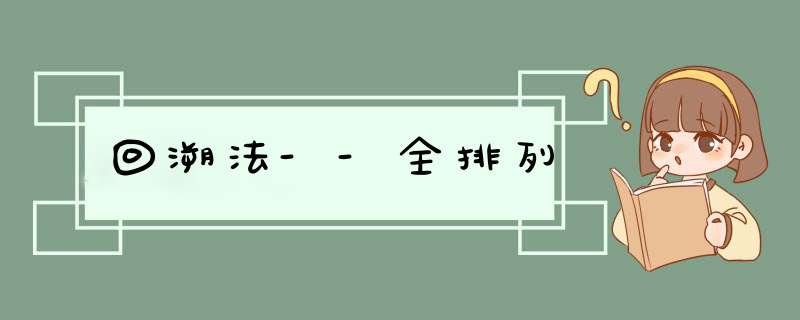
a=[1,2,3]n=len(a)res=[]def permutation(a,solution):    #注意，这里要用global修饰res，才能更新结果    global res    if len(a)==0:        res.append(solution)        return    for i in range(len(a)):
　　　　　newsolution=solution+[a[i]]        new_a=a[:i]+a[i+1:]        permutation(new_a,newsolution)permutation(a,[])print(res)输出：[[1,3],[1,3,2],[2,1,1],[3,1]]

基本思路：

其实对于回溯法，我们要从反向开始考虑。我们每次从原始数组中选择一个加入到结果中，当原始数组中（新建的）没有元素时（也就是len(a)==0，此时结果为[1,3]），我们得到了第一个排列，我们将这个排列加入到结果集中，然后返回上一步，也就是我们现在有[1,2]，再返回一步[1]，此时再加入3，再加入2，得到[1,

以此类推。

总结

以上是内存溢出为你收集整理的回溯法--全排列全部内容，希望文章能够帮你解决回溯法--全排列所遇到的程序开发问题。

如果觉得内存溢出网站内容还不错，欢迎将内存溢出网站推荐给程序员好友。