f(x)关于(1,0)对称有哪些性质

函数关于（1,0）对称,说明什么

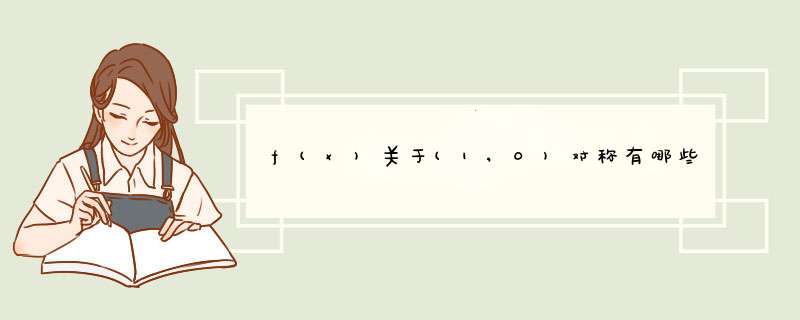
答案: （x,f(x)）关于（1,0）的对称点为（2-x,-f(x)）,有f(2-x)=-f(x)=f(-x),所以函数为周期函数,且2为其一个周期综述如下：（1，0）是一个点。函数图象关于一个点对称，自然是指中心对称。

即如果（x1，F（x1））是图象上一个点，则必然存在图象上另一点（x2，F（x2））使得：（x1+x2）／2=1，（F（x1）＋F（x2））／2=0即x2= 2-x1，F（x2）＝－F（x1）．令x2=-x，带入得F（－x）＝－F（－2+x）。

方程分类

代数学中，根据方程未知数的个数，可将其分为：一元方程，二元方程，三元方程等。根据方程未知项的最高次数，可将其分为：一次方程，二次方程，三次方程等。在近代数学中，还有微分方程、差分方程、积分方程等学科。此外，还可以将方程分为线性方程和非线性方程。

f(x)+f(-x)=2为什么关于(0,1)对称

关於(0,1)对称,则垂直渐近线是x = 0,水平渐近线是y = 1f(x) = g(x) + 1,g(x)是奇函数f(- x) = g(- x) + 1 = - g(x) + 1f(x) + f(- x) = [g(x) + 1] + [- g(x) + 1] = 2例子：f(x) = 1/x + 1、f(x) = - 1/x + 1其他情况有关於原点(0,0)对称,则函数是f(x) = g(x)形式关於(0,k)对称,则函数是f(x) = g(x) + k形式因为对称关系,所以g都是奇函数茹菓关於(h,0)对称的话,则是f(y) = g(y) + h形式

说一次再见吧

高中数学解题技巧主要有以下几种方法：  

1、配方法：把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和形式。  

2、因式分解法：因式分解，就是把一个多项式化成几个整式乘积的形式。

 3、换元法：所谓换元法，就是在一个比较复杂的数学式子中，用新的变元去代替原式的一个部分或改造原来的式子，使它简化，使问题易于解决。

4、判别式法与韦达定理：一元二次方程ax2+bx+c=0（a、b、c属于R，a≠0）根的判别，△=b2-4ac，。韦达定理除了已知一元二次方程的一个根，求另一根；已知两个数的和与积，求这两个数等简单应用外，还可以求根的对称函数。

孩子数学学不好的原因：  

1、不要让孩子被动学习，还有很多同学在上了高中之后还想初中，那样每天吊儿郎当，这是跟随着老师的思路。自己没有一些衍生，之前没有学习方法，在下课了也不会找。

2、老师上课的时候就是把这个知识表达的清楚一点，分析一下重点和难点。然而还有很多学生上课不专心听课。对很多要点也都不知道，只是笔记记了一大堆，自己也看不懂问题还有很多，在课后也不会进行总结。