增（减）函数相加减得到的函数各是什么? 增（减）函数相乘除得到的函数各是什么?

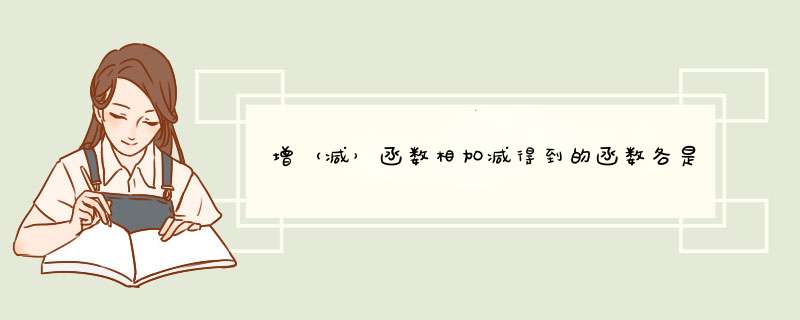
我有如下答案：

增+增=增

增-减=增

减+减=减

（其他无法确定）

相乘除则

增减乘除得减

增增,减减乘除得增

增函数X增函数后的函数是未定的，你述说中的判定是不存在的，也就是说，增函数之积不一定是增函数。下面给出证明

证明：

设y1=f(x)和y2=g(x)都是定义域上的增函数，而且f(x)和g(x)定义域相交不为空集，设其定义域的交集为A，函数y=f(x)g(x)有y1和y2组成，则：

令x1，x2∈A，且x1<x2，则：

f(x1)<f(x2)和g(x1)<g(x2)恒成立，

但是f(x1)g(x1)与f(x2)g(x2)的关系是不能确定的，因为很显然：

当f(x1),f(x2),g(x1),g(x2)中有小于零时，

f(x1)g(x1)<f(x2)g(x2)不一定成立，即：

f(x1)g(x1)和f(x2)g(x2)的关系不能判定，

因此，增函数之积构成的新函数单调性不能确定

从上述证明也可以看出，如果要增函数之积构成的函数是增函数成立，必须是这两个增函数都大于零，即：

当y1=f(x)和y2=g(x)大于零恒成立，且满足：

①f(x)和g(x)都是增函数；

②定义域交集不为空集；

则：y=f(x)g(x)也是增函数

两个增函数相乘不一定是增函数

举个简单的例子

y(x)=x+1是增函数

g(x)=x-1也是增函数

两函数相乘假设得到函数f(x)

那么f(x)=（x+1）（x-1）= x² -1

该函数

在定义域0，+∞）上为增函数

在定义域（-∞，0）上为减函数

扩展资料：

判断函数单调性的基本方法有：

①定义法

②图像法

③复合函数法

④导数法等等。

而定义法和导数法是做题中最常用的两种方法。

定义法

根据定义，我们可以归纳出用定义法证明函数单调性的思路为：

1）取值：设  

为该相应区间的任意两个值，并规定它们的大小，如  ；

2）作差：计算  ，并通过因式分解、配方、有理化等方法作有利于判断其符号的变形；

3）定号：判断  的符号，若不能确定，则可分区间讨论；

4）结论：根据差的符号，得出单调性的结论。

导数法

一般地，对于给定区间上的函数  ，如果  ，那么就说  在这个区间上是增函数；

如果  ，那么就说  在这个区间上是减函数。

我们也可以归纳出用导数法证明函数单调性的基本思路：

一般应先确定函数的定义域，再求导数，通过判断函数定义域被导数为零的点（  ）所划分的各区间内  的符号来确定函数  在该区间上的单调性。

参考资料：

1

增函数乘以增函数是增函数不一定是增函数

如f(x)=x在r上是增函数

g(x)=x在r上是增函数

而f(x)g(x)=x^2在r上不是增函数

2

复合增函数也一定是增函数

令f(x)=x在f上是增函数,

g(x)=x在g上是增函数,二者复合函数f(g(x))在g上有意义

令x1,x2在g上,x1<x2

则g(x1)<g(x2)

f(g(x1))<f(g(x2))