求y=e^x—e^-x2的反函数，反函数是奇函数还是偶函数，在零到正无穷上是增还是减。要详细！！

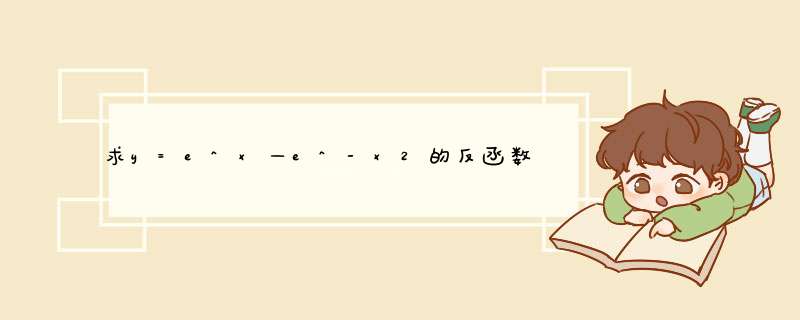
y=(e^x-e^(-x))/2，双曲正弦函数。

解：∵y=(e^x-e^(-x))/2 =>2y=e^x-e^(-x)

=>2ye^x=e^(2x)-1

=>e^(2x)-2ye^x=1

=>e^(2x)-2ye^x+y²=1+y²

=>(e^x-y)²=1+y²

=>e^x-y=±√(1+y²)

=>e^x=y±√(1+y²)

=>x=ln│y±√(1+y²)│

=>x=±ln│y+√(1+y²)│ (∵ln│y-√(1+y²)│=-ln│y+√(1+y²)│)

=>x=±ln(y+√(1+y²)) (∵y+√(1+y²)>0)

∴原函数的反函数是 x=±ln(y+√(1+y²))。

此函数是反双曲正弦函数，定义域为(-∞，﹢∞)，它是奇函数，在区间内单调增加。

y＝lnx

分析：

反函数就是让x，y掉转。因为y=e^x，所以两边取对数有lny=xlne。

lne=1，所以lny=x，令x＝y，y＝x，所以y=e^x的反函数是y＝lnx。

扩展资料：

反函数的性质：

（1）函数存在反函数的充要条件是，函数的定义域与值域是一一映射；

（2）一个函数与它的反函数在相应区间上单调性一致；

（3）大部分偶函数不存在反函数（当函数y=f(x)， 定义域是{0} 且 f(x)=C （其中C是常数），则函数f(x)是偶函数且有反函数，其反函数的定义域是{C}，值域为{0} ）。

奇函数不一定存在反函数，被与y轴垂直的直线截时能过2个及以上点即没有反函数。若一个奇函数存在反函数，则它的反函数也是奇函数。

（4）一段连续的函数的单调性在对应区间内具有一致性；

（5）严增（减）的函数一定有严格增（减）的反函数；

（6）反函数是相互的且具有唯一性。

(1)

y=(1－x)/(1＋x)

y(1＋x)=1－x

y＋xy=1－x

xy＋x=1－y

x(y＋1)=1－y

x=(1－y)/(y＋1)

这个函数的反函数是：y=(1－x)/(x＋1) (x≠－1)

(2)

y=[e^x－e^(－x)]/2

2y=e^x－e^(－x) --------------------------①

两边平方,得：

4y²=[e^x－e^(－x)]²

4y²＋4=[e^x－e^(－x)]²＋4=[e^x＋e^(－x)]²

得：

√(4y²＋4)=e^x＋e^(－x) ---------------②

①＋②,得：

2y＋2√(y²＋1)=2e^x

e^x=y＋√(y²＋1)

x=ln[y＋√(y²＋1)]

原函数的反函数是：y=ln[x＋√(x²＋1)]

y=e^x

lny=lne^x

x=lny

y=e^x的反函数是：y=lnx

朋友，请采纳正确答案，你们只提问，不采纳正确答案，回答都没有劲！！！

朋友，请采纳答案，您的采纳是我答题的动力，如果没有明白，请追问。谢谢。