用matlab拟合一组数据，函数的表达式是什么？

用MATLAB拟合一组数据，得到函数的表达式我的数据是

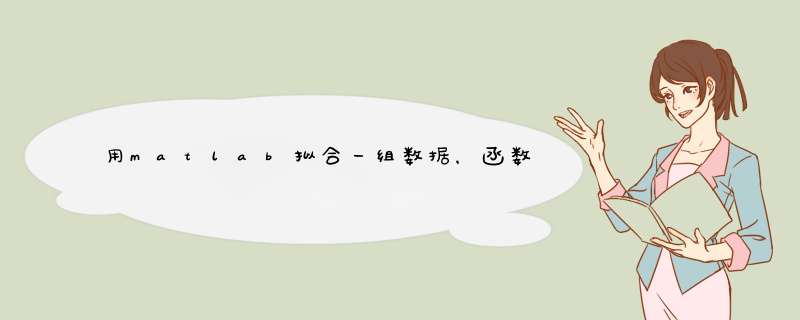
x=（9，11，13，15，17，19，21，23，25，27，29，31，33，35，37，39）

y=（9，12，18，21，12，26，29，36，50，101，192，245，233，117，28，9）

至于具体怎么得到x与y的函数关系,在MATLAB上的具体 *** 作，可能性太多，这组数据可以拟合出无数多种函数结果。

如果什么函数形式都不给出的话，下面以11次多项式举例来拟合你的数据：

1用多项式拟合

x=（9，11，13，15，17，19，21，23，25，27，29，31，33，35，37，39）

y=（9，12，18，21，12，26，29，36，50，101，192，245，233，117，28，9）

p=polyfit（x，y，11）

xx=linspace（9，39，100）

yy=polyval（p，xx）

plot（x，y，'o'）；hold on

plot（xx，yy，'r'）；hold off

legend（'数据','拟合','location','northwest'）；

title（poly2str（p,'x'））;

2如果是正态分布

x=（9，11，13，15，17，19，21，23，25，27，29，31，33，35，37，39）

y=（9，12，18，21，12，26，29，36，50，101，192，245，233，117，28，9）

fun=@(p,x) p(1)exp(-(x-p(2))^2/2/p(3)^2);

p=nlinfit(x,y,fun,[250 32 10]);

xx=linspace(9,39,100);

yy=fun(p,xx);

plot(x,y,'o');hold on

plot(xx,yy,'r');hold off

legend('数据','拟合','location','northwest');

MATLAB是matrix&laboratory两个词的组合，意为矩阵工厂（矩阵实验室）。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。

根据给定的数据，我们可以假定函数表达式为

y=b1+b2x+b3x^2+b4x^3+b5x^4;

所以上述函数可以用matlab的regress（）多元线性回归分析函数来拟合。实现过程如下：

A=[175,026;225,032;25,044;2875,057;2686,050;2563,046];

x=A(:,1)，y=A(:,2)

X=[ones(length(y),1),x,x^2,x^3,x^4];

b=regress(y,X)

x1=linspace(15,3,50);

y1=b(1)+b(2)x1+b(3)x1^2+b(4)x1^3+b(5)x1^4;

plot(x,y,'k',x1,y1,'r-')

grid on

xlabel('x'),ylabel('y')

运行结果

如下：

function

fit_tulun 

%多项式拟合方式

x=linspace(0,4pi,6); 

y_jingque=sin(x);

%决定稀疏样本点数据

p_poly=polyfit(x,y_jingque,5); 

x_poly_fit=linspace(0,4pi,100); 

y_poly_fit=polyval(p_poly,x_poly_fit); 

%三次样条拟合方式

sp=csapi(x,y_jingque); 

%求三次样条函数的导数 

s_diff=fnder(sp,1); 

plot(x_poly_fit,y_poly_fit,'ko',x_poly_fit,y_poly_fit,'b:') 

%plot(x_poly_fit,y_poly_fit,'b:') 

hold

on 

fnplt(sp,'r') 

fnplt(s_diff,'c') 

x1=linspace(0,4pi,200); 

plot(x1,sin(x1),'m','linewidth',18) 

legend('多项式拟合样本点','多项式拟合曲线','三次样条拟合曲线','三次样条导数曲线','正弦曲线精确图形')