分类算法 - SVM算法

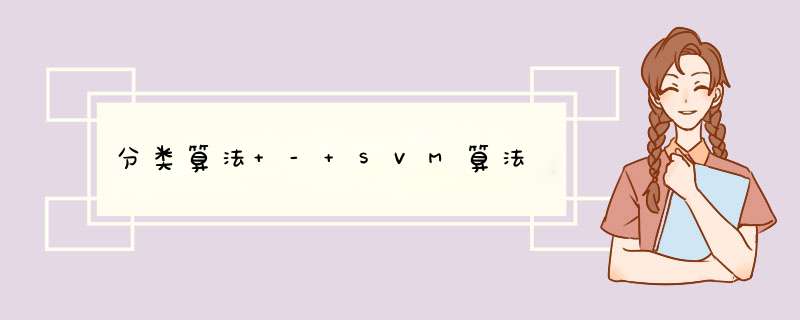
SVM的全称是Support Vector Machine，即支持向量机，主要用于解决模式识别领域中的数据分类问题，属于有监督学习算法的一种。SVM要解决的问题可以用一个经典的二分类问题加以描述。如图1所示，红色和蓝色的二维数据点显然是可以被一条直线分开的，在模式识别领域称为线性可分问题。然而将两类数据点分开的直线显然不止一条。图2和3分别给出了A、B两种不同的分类方案，其中黑色实线为分界线，术语称为“决策面”。每个决策面对应了一个线性分类器。虽然在目前的数据上看，这两个分类器的分类结果是一样的，但如果考虑潜在的其他数据历带，则两者的分类性能是有差别的。

之前在b站看到一个非常好的介绍！！十分推荐， 这是传送门

按照我自己的理解，以二维数据为例，我们喂给模型已经分类好的数据乱袜，那么假设有一线条可以将此部分数据正确划分为2大部分，这样可以形成2个等式，即横线两边的数值归类为1或者-1，一般情况下可以求出最大间隔即无数个解，因此需要一个限定条件求出最优的那条线条。限定方式为：无数个解形成一个解的范围，距离边缘相等的那条线条即是最优解。

有时候本来数据的确是可分的，也就是说可以用线性分类SVM的学习方法来求解，但是却因为混入了异常点，导致不能线性可分，比如下图，本来数据是可以按下面的实线来做超平面分离的，可以由于一个橙色和一个蓝色的异常点导致我们没法按照线性分类支持向量机方法来分类。

以上讨论的都是在线性可分情况进行讨论的，但是实际问题中给出的数据并不是都是线性可分的，比如有些数据可能是曲线的。

那么这种非线性可分的数据是否就不能用SVM算法来求解呢？答案是否定的。事实上，对于低维平面内不可分的数据，放在一个高维空间中去就有可能变得可分。以二维平面的数据为例，我们可以通过找到一个映射将二维平面的点放到三维平面之中。理论上任意的数据样本都能够找到一个合适的映射使得这些哗烂激在低维空间不能划分的样本到高维空间中之后能够线性可分。

当特征变量非常多的时候，在高维空间中计算内积的运算量是非常庞大的。考虑到我们的目的并不是为找到这样一个映射而是为了计算其在高维空间的内积，因此如果我们能够找到计算高维空间下内积的公式，那么就能够避免这样庞大的计算量，我们的问题也就解决了。实际上这就是我们要找的 核函数 ，即两个向量在隐式映射后的空间中的内积。

（1）对于边界清晰的分类问题效果好；

（2）对高维分类问题效果好；

（3）当维度高于样本数的时候，SVM 较为有效；

（4）因为最终只使用训练集中的支持向量，所以节约内存

（1）当数据量较大时，训练时间会较长；

（2）当数据集的噪音过多时，表现不好；

（3）SVM 不直接提供结果的概率估计，它在计算时直接使用 5 倍交叉验证。

（1）LR 与 SVM 都是分类算法；

（2）LR 与 SVM 都是监督学习算法；

（3）LR 与 SVM 都是判别模型；

（4）关于判别模型与生成模型的详细概念与理解，笔者会在下篇博文给出，这里不详述。

（5）如果不考虑核函数，LR 与 SVM 都是线性分类算法，也就是说他们的分类决策面都是线性的

这里需要说明的是，LR 也是可以用核函数的，因在 LR 算法里，每个样本点都必须参与决策面的计算过程，也就是说，如果在 LR 里也运用核函数的原理，那么每个样本点都必须参与核计算，这带来的计算复杂度是相当高的。所以在具体应用时，LR 很少运用核函数机制。

（1）损失函数不同；

（2）SVM 只考虑支持向量，而 LR 考虑全局（即远离的点对边界线的确定也起作用）；

（3）在解决非线性问题时，SVM 采用核函数的机制，而 LR 通常不采用核函数的方法；

（4）SVM 的损失函数就自带正则（损失函数中的12||w||2项），这就是为什么 SVM 是结构风险最小化算法的原因，而 LR 必须另外在损失函数上添加正则项；

（5）LR是参数模型，SVM是非参数模型，本质不同。

（6）在训练集较小时，SVM 较适用，而 LR 需要较多的样本。

（1）LR 与线性回归都是广义的线性回归；

（2）线性回归模型的优化目标函数是最小二乘，而 LR 则是似然函数；

（3）线性回归在整个实数域范围内进行预测，敏感度一致，而分类范围，需要在[0,1]。逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型，因而对于这类问题来说，逻辑回归的鲁棒性比线性回归的要好。

（4）逻辑回归的模型本质上是一个线性回归模型，逻辑回归都是以线性回归为理论支持的。但线性回归模型无法做到 sigmoid 的非线性形式，sigmoid 可以轻松处理 0/1 分类问题。

（5）线性回归主要做预测，LR 主要做分类（如二分类）；

支持向量机（英语：support vector machine，常简称为SVM，又名支持向量网络）是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。

SVM使用铰链损失函数（hinge loss）计算经验风险（empirical risk）并在求解系统中加入了正则化项以优化结构风险（structural risk），是一个具有稀疏性和稳健性的分类器。

SVM可以通过核方法（kernel method）进行非线性分类，是常见的核学习（kernel learning）方法之一 。

SVM被提出于1964年，在二十世纪90年代后得到快速发展并衍生出一系列改进和扩展算法，在人像识别、文本分类等模式识别（pattern recognition）问题中有得到应用。

动机

H1 不能把类别分开。H2 可以，但只有很小的间隔。H3 以最大间隔将它们分开。

将数据进行分类是机器学习中的一项常见任务。 假设某些给定的数据点各自属于两个类之一，而目标是确定新数据点将在哪个类中。对于支持向量机来说，数据点被视为p 维向量，而我们想知道是否可以用 (p-1)维超平面来分开这些点。

这就是所谓的线性分类器。可能有许多超平面可以把数据滚数唯分类。最佳超平面的一个合理选择是以最大间隔把两个类分开的超平面。

因此，我们要选择能够让到每边最近的数据点的距离最大化的超平面。如果存在这样的超平面，则称为最大间隔超平面，而其定义的线性分类器被称为最大间隔分类器，或者叫做最佳稳定性感知器。

应用

1、用于文本和超文本的分类，在归纳和直推方法中都可以显著减少所需要的有类标的样本数。

2、用于图像分类。实验结果显示：在经过三到四轮相关反馈之后，比起传统的查询优化方案，支持向量机能够获取明显更高的搜索准确度。这同样也适用于图大培像分割系统，比如使用Vapnik所建议的使用特权方法的修改版本SVM的那些图像分割系统。

3、用于手写字体识别。

4、用于医学中分类蛋白质，超过90%的化合物能够被正确分类。基于支持向量机权毕歼重的置换测试已被建议作为一种机制，用于解释的支持向量机模型。

支持向量机权重也被用来解释过去的SVM模型。为识别模型用于进行预测的特征而对支持向量机模型做出事后解释是在生物科学中具有特殊意义的相对较新的研究领域。

以上内容参考 百度百科-支持向量机

SVM算法中文翻译为支持向量机，它的英文全称是Support Vector Machine。

之所以叫作支持向量机，基厅是因为该算法最终训练出来的模型，由一些支持向量决定。所谓的支持向量，也就是能够决定最终模型的向量。SVM算法最初是用来解决二分类问题的，而在这个基础上进行扩展，也能够处理多分类问题以及回归问题。

SVM算法的历史

早在1963 年，著名的前苏联统计学家弗拉基米尔·瓦普尼克在读博士期间，就和他的同搏燃隐事阿列克谢·切尔沃宁基斯共同提出了支持向量机的概念。

但由于当时的国际环境影响，他们用俄文发表的论文，并没有受到国际学术界的关注。直到 20 世纪 90 年代，瓦普尼克随着移民潮来到美国，而后又发表了 SVM 理论。此后，SVM 算法才受段谈到应有的重视。如今，SVM 算法被称为最好的监督学习算法之一。

---