如图,在RT△ABC中,∠ABC=90°,AC=BC,M,N为BC上的点,且CM=BN,过C作AM的垂线交AB于E,D为垂足

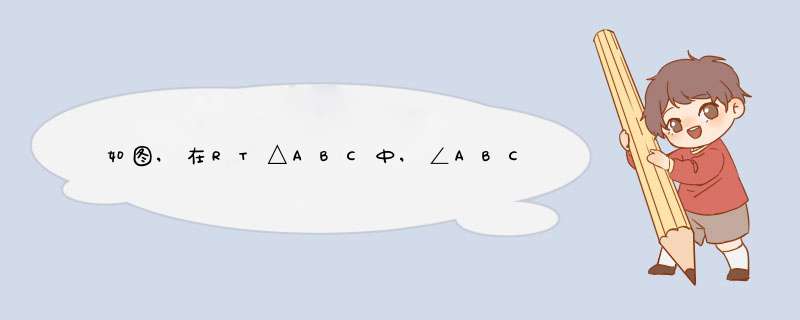
证明要点：

作CG⊥AB，交AM于H

根据等腰直角三角形及CD⊥AM的条件可证：

∠CAM＝∠BCE，∠ACG＝∠B，AG＝BG

又AC＝BC

所以△ACH≌△CBE（ASA）

所以CH＝BE，AH＝CE

所以GH＝GE

所以△GEH是等腰直角三角形　

所以∠CHE＝∠BEH＝135度

因为CM＝BN，∠BCG＝∠B＝45度

所以△CMH≌△BNE（SAS）

所以∠CHM＝∠BEN

所以∠FHE＝∠FEH

所以EF＝HF

所以AF＝AH＋HF＝CE＋EF

江苏吴云超解答　供参考！

分析：

（1）由条件可以通过三角形全等和轴对称的性质，直角三角形的性质就可以得出结论；

（2）取AB、AC的中点F、G，连接DF,MF,EG,MG,根据三角形的中位线的性质和等腰直角三角形的性质就可以得出四边形AFMG是平行四边形，从而得出三角形DGM全等于三角形MGE，根据其性质就可以得出结论；

具体解题过程你可以参考下图：

∵∠ACD＝∠ACB+∠BCD，∠BCE＝∠DCE+∠BCD，∠ACB＝∠DCE

∴∠ACD＝∠BCE

∵AB＝AC，CD＝CE

∴△ACD≌△BCE （SAS）

∴AD＝BE，S△ACD＝S△BCE

∵CP⊥BE，CQ⊥AD

∴S△ACD＝AD×CQ/2, S△BCE＝BE×CP/2

∴AD×CQ/2＝BE×CP/2

∴CP＝CQ

∴CH平分∠AHE

2、解：将AD与BC的交点设为M，CD与BE的交点设为N

∵△ACD≌△BCE

∴∠A＝∠B，∠D＝∠E

∵∠A+∠D+∠ACD＝180，∠ACD＝∠ACB+∠BCD

∴∠BCD＝180-（∠A+∠D+∠ACB）

∵∠CMH＝∠A+∠ACB，∠CNH＝∠E+∠DCE，∠AHE+∠BCD+∠CMH+∠CNH＝360

∴∠AHE+180-（∠A+∠D+∠ACB）+∠A+∠ACB+∠E+∠DCE＝360

∴∠AHE＝180-∠DCE＝180-α

∵CH平分∠AHE

∴∠CHE＝∠AHE/2＝90-α/2

证明：延长CH与AB相交于点M，连接CG,MG

因为ABCD是正方形

所以角ABC=90度

DC=BC

DC平行AB

所以角CDH=角MFH

角HCD=角HMF

因为点H是DF的中点

所以DH=FH

所以三角形DCH和三角形FMH全等（AAS)

所以CH=MH

DC=FM

所以BC=FM

因为BEFG是正方形

所以角GBF=角MFG=45度

BG=FG

因为角ABC+角CBG+角GBF=180度

所以角CBG=45度

所以角CBG=角MFG=45度

所以三角形CBG和三角形FMG全等（SAS)

所以CG=MG

所以三角形CMG是等腰三角形

因为CH=MH

所以GM是等腰三角形CGM的中线

所以GH是等腰三角形CGM的垂线

所以GH垂直CH

以上就是关于如图,在RT△ABC中,∠ABC=90°,AC=BC,M,N为BC上的点,且CM=BN,过C作AM的垂线交AB于E,D为垂足全部的内容，包括:如图,在RT△ABC中,∠ABC=90°,AC=BC,M,N为BC上的点,且CM=BN,过C作AM的垂线交AB于E,D为垂足、初中几何证明问题，在线等……、如图，CA=CB,CD=CE,ACB=DCE=α。AD,BE交于点H，连CH，求证：角CHE的度数等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！