MATLAB中脉冲函数是什么

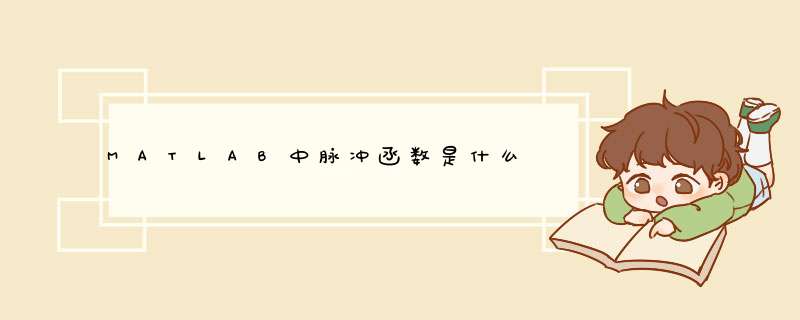
clear all;t1=-05:0001:0;A=50;A1=1/50;n1=length(t1);u1=zeros(1,n1);t2=0:0001:A1;t0=0;u2=Astepfun(t2,t0);t3=A1:0001:1;n3=length(t3);u3=zeros(1,n3);t=[t1,t2,t3];u=[u1,u2,u3];plot(t,u);axis([-05 1 0 A+2])这个是dirac函数

脉冲函数

impulse function

时域内被采函数的另一数学表达式f’(t):f’(t)=厶f(t(k))6(t—t(k))(1—2)其中t(k)为函数被采样时刻,6(1)为D[I~Cdelta函数或称为脉冲函数,

冲击函数平衡法主要是根据微分方程两边含有的冲激函数和其各阶导数来配平。

将h(t)=(齐次解形式)u(t)+δ(t)的从0到(m-n)阶的各阶导数的线性组合，即各阶导数乘以1个待定系数，代入方程的y(t)，f(t)代入δ(t)；通过让方程两端的δ(t)各阶导数的系数相等，即匹配，求出h(t)。

扩展资料：

冲击函数匹配法的原理：

1狄拉克（Dirac）给冲激函数这样定义{█(∫_(-∞)^∞▒〖δ(t)=1〗,&@δ(t)=0,&t≠0)┤。

2△u(t)={█(0 ，t≤0@1 ，t=0_+@0 ，t>0_+ )┤。

在这里△u（t）可视为常数1。即∫_(0_- )^(0_+)▒〖△u（t）dt〗=1。

3 △u(t)的微分是δ(t)。

我们应该知道冲激函数匹配法，本质上就是根据等式左右两端的阶数应相同。等式一般为含有冲激函数或其导数的微分方程。下面我将给出一个例子用来解释。

d/dt r(t)+3r(t)=3δ’(t)

右式含有δ’(t)函数，所以左式最高阶次的导数即r’(t)应该含有δ’(t)。可能有的读者不理解，我们不妨反证一下，如果r(t)含有δ’(t)，那r’(t)就得δ‘’(t)，这样的话等式左右两端就不平衡了。

下面我们来推导一下d/dt r(t)和r(t)、我们不妨先设d/dt r(t)=3 δ’(t)、那么r(t)=∫_(-∞)^t▒〖d/dt r(t)〗=3δ(t) 。

将以上②③式代入①，发现等式不平衡d/dt r(t)应该补充一项，即d/dt r(t)= 3δ’(t)-9δ(t)，那么r(t)=3δ(t)-9△u(t)，再重复代入的步骤，最后得d/dt r(t)= 3δ’(t)-9δ(t)+ 27△u(t)、r(t)=3δ(t)-9△u(t)。

了解以上推导的过程后，我们可以总结出一种更简便的方法，即待定系数法法。还是用上面①式的微分方程为例。

d/dt r(t)+3r(t)=3δ’(t)、设d/dt r(t)= aδ’(t)+bδ(t)+ c△u(t)、那么r(t)=aδ(t)+b△u(t)、将d/dt r(t) r(t)代入微分方程。

对应系数相等得{█(a=3@b+3a=0@3b+c=0)┤ 解{█(a=3@b=-9@c=27)即d/dt r(t)= 3δ’(t)-9δ(t)+ 27△u(t)。r(t)=3δ(t)-9△u(t)。

方法一：

在Simulink中有专门的生成阶跃信号和冲击信号的模块

方法二：

function y=sstep(t,s,t0,a0,a1)

% 此程序用于生成阶跃信号

% t 总时长

% s 步长

% t0 阶跃开始时刻

% a0 阶跃前幅值

% a1 阶跃后的幅值

j=0;

for i=0:s:t

j=j+1;

if i < t0

y(j)=a0;

else

y(j)=a1;

end

end

冲击信号你可以如法炮制。

方法三：

你也可以这样做：

% Matlab中符号计算中提供

% 单位阶跃函数heaviside(t-a)

% 单位脉冲函数dirac(x-a)

% 至于斜坡可以使用阶跃和直线方程构成

%

%比如要绘制a=4时的阶跃函数

f=@(t)heaviside(t-4);

ezplot(f,[0 5])

%

%绘制a=2时的脉冲信号

f=@(x)dirac(x-2);

ezplot(f,[0 5])%这个在图形上没法显示

就我所知，matlab里面应该没有dirac这个函数，这个函数应该是自己定义的一个关于w的函数。

至于ifourier(f,w,x)则等同于f(x) = 1/(2pi) int(F(w)exp(iwx,w,-inf,inf),这里F为关于w的函数（一般都是默认为w的函数）

相当于做逆傅里叶变换后的函数。

以上就是关于MATLAB中脉冲函数是什么全部的内容，包括:MATLAB中脉冲函数是什么、《信号与系统》中冲击函数匹配法的具体内容及怎样用、阶跃信号是冲激信号的积分，用方程计算的话，怎么算啊等相关内容解答，如果想了解更多相关内容，可以关注我们，你们的支持是我们更新的动力！