ab=ba的充要条件

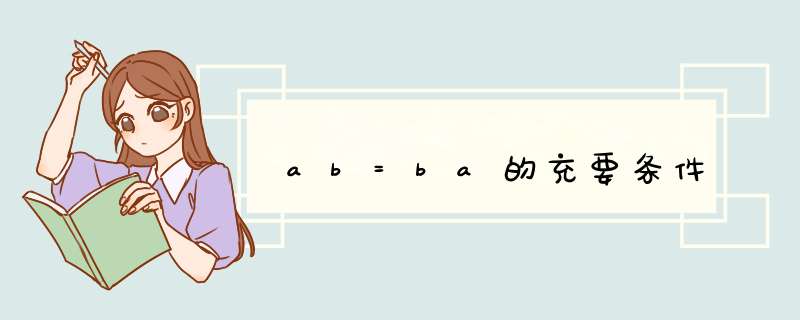
AB是对称矩阵，则AB=BA的充要条件是A，B都为对称矩阵。两个对称矩阵的积是对称矩阵，当且仅当两者的乘法可交换。两个实对称矩阵乘法可交换当且仅当两者的特征空间相同。

1、相似的定义为：对n阶方阵A、B,若存在可逆矩阵P,使得P^(-1)AP=B,则称A、B相似.

2、从定义出发,最简单的充要条件即是：对于给定的A、B,能够找到这样的一个P,使得：

P^(-1)AP=B；或者：能够找到一个矩阵C,使得A和B均相似于C.

3、进一步地,如果A、B均可相似对角化,则他们相似的充要条件为：A、B具有相同的特征值.

4、再进一步,如果A、B均为实对称矩阵,则它们必可相似对角化,可以直接计算特征值加以判断（与2情况不同的是：2情况必须首先判断A、B可否相似对角化）.

5、以上为线性代数涉及到的知识,而如果你也学过矩阵论,那么A、B相似的等价条件还有：

设：A、B均为n阶方阵,则以下命题等价：

(1)A~B