
1981年,日本的Nabae等人提出了多电平变换器的思想,近年来成为了高压大功率变频领域的一个研究热点。多电平逆变器输出电压阶梯多,从而可以使输出的电压波形具有较小的谐波和较低的du/dt。随着输出电平数的增加,输出电压的谐波将减少。另外,多电平逆变技术在减小系统的开关损耗与导通损耗,降低管子的耐压与系统的EMI方面性能都非常优良。
传统的多电平逆变器可分为二极管箝位型、电容箝位型以及级联型等三种结构拓扑,二极管箝位型逆变器因为在随着电平数的增多,其开关器件和箝位二极管会大量的增加,因此通常只适合于五电平以下的多电平拓扑。而电容箝位型逆变器存在有电容的充放电电压平衡的问题,而且在电平数增加时,会需要较多的箝位电容,因此也存在一定的弱点。 对级联型多电平逆变器来说,当需要得到多个电平时,会需要较多的直流电源,整流侧会需要一组变压器,造成体积庞大,另外也不易实现四象限运行。
针对传统多电平拓扑结构的上述不足,本文提出了一种新的不对称混合多电平逆变器结构,通过控制输入端的电源数目,可以得到不同的电平数,最多可以得到六个输出电平,在减少器件与直流电压源的同时,增加了电平数的输出。
l 逆变器的运行原理分析
逆变器的结构原理图如图1所示,从该图可以看到,电源侧一共由三个直流电源组成,桥臂左侧由两电平半桥单元组成,桥臂右侧由一个三电平半桥单元组成,分别箝位在中间电源V2上与直流总线电源上。三电平半桥即是普通的二极管箝位三电平半桥。中性点N通过导线连到箝位二极管的中点处。V1,V2,V3分别代表三个直流电源,其中V2通过两个电容C2,C3分压,V1,V2,V3的不同的比值将在负载端AO出现不同的电平。当V1:V2:V3=3:2:3时,可以得到最多六个电平的输出,此时,我们可以看到两个单元的直流电压都按照最大扩展原则来确定的,得到了最大电平数2×3=6的输出。
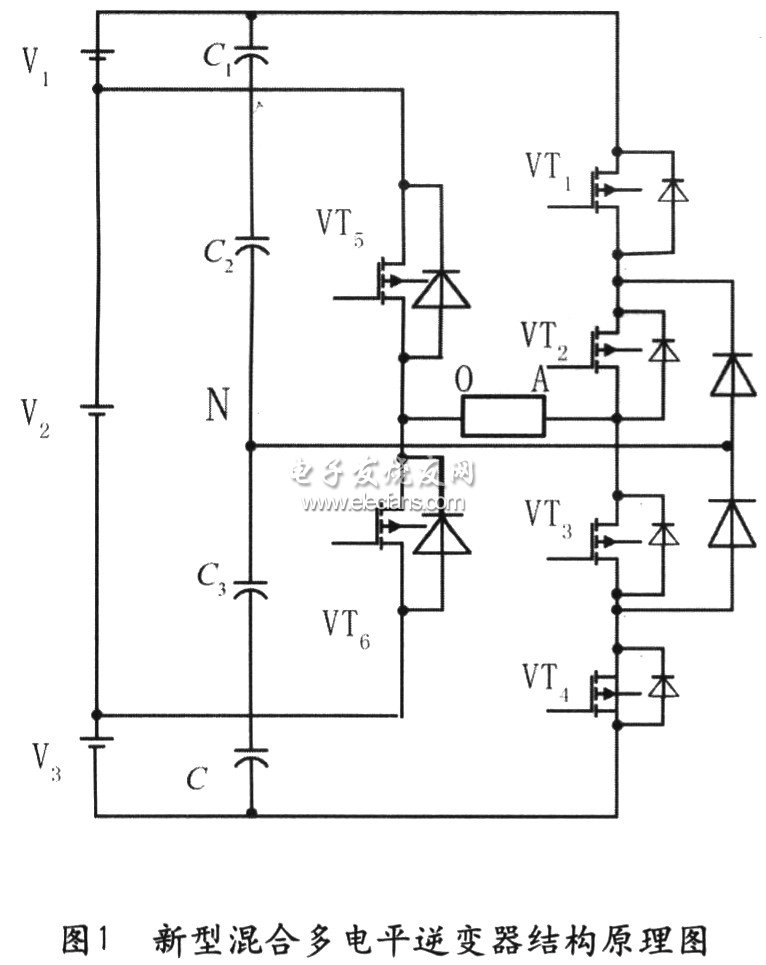
当电压比Vl:V2:V3=3:2:3时,负载AO上得到的六电平输出电压状态与各器件导通状态的关系如表1所示。设单位电压为V。时,得到的输出电压为+Vd,一Vd,+3Vd,一3Vd,+5Vd,一5Vd。
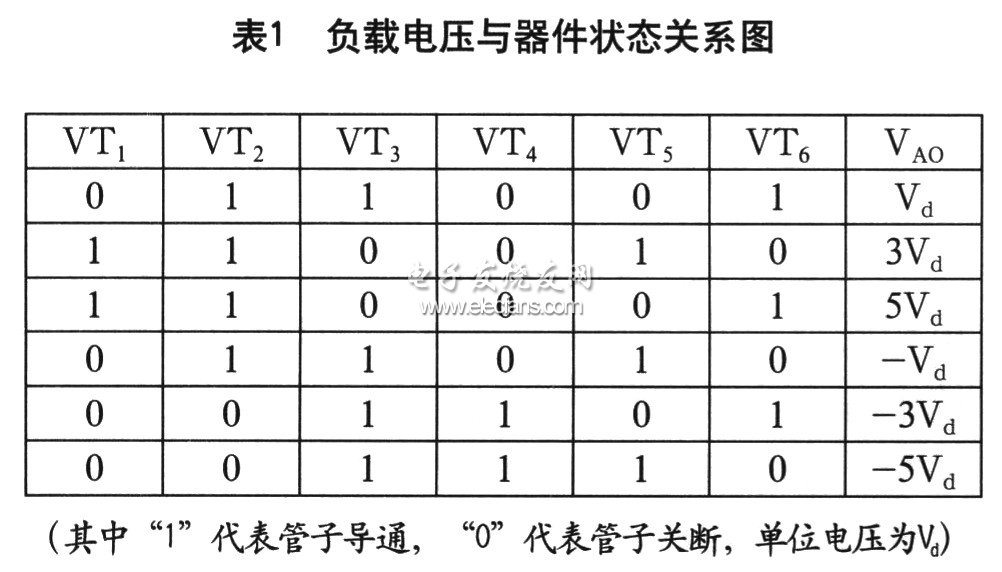
当电压比V1:V2:V3=l:2:1时,可以得到四电平的输出,输出电平为+Vd,一Vd,+2Vd,一2Vd。
从状态图我们可以看到,负载电压与器件状态的关系。管子VT2与VT3的导通时间明显要长于其他器件,而VT5与VT6的开关次数要多,但耐压要低。在一个多电平系统中,根据器件的特性,应合理选择器件,左侧两电平单元可以选用耐压相对低一些的,而右侧三电平单元则需要耐压高导通损耗低的器件。
本文对所提出的新型混合六电平逆变器与传统五电平逆变器在主电路结构上进行了比较,见表2。
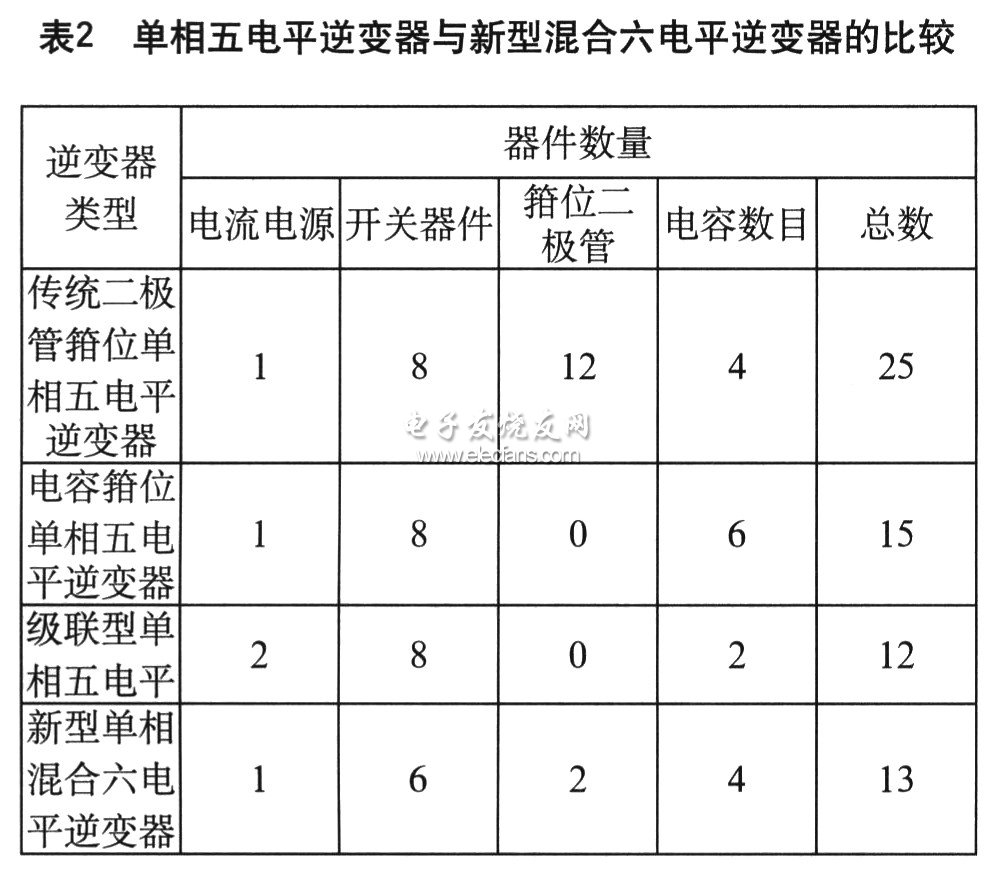
从表2中我们可以看出新型混合六电平逆变器要明显优于传统的六电平逆变器,可以明显的节省器件、降低系统的损耗。作为六电平逆变器还可以极大的降低输出电压的谐波含量,改善输出电压波形质量。与五电平逆变器不同的是,六电平逆变器输出电压没有零电平。
2 逆变器的调制原理
一种拓扑结构,必须采用合适的调制方法,才能得到期望的输出。不同主电路结构的逆变器,都对应有一定的调制方式。在本文所提出的新型混合六电平逆变器中,采用特定谐波消除法(SHEPWM)作为该拓扑结构的调制方式。能够极大地降低系统的开关频率,从而减低损耗。该方法的基本思想是通过傅立叶级数分析,得出在特定开关角下的傅立叶级数展开式,然后令某些特定的低次谐波为零,从而得到一个反映Ⅳ个开关角的N个非线性独立方程,按求解的开关角进行控制,则必定不含这些次数的谐波。通常,这种方法着眼于消除低次谐波,因为高次谐波幅值较小,同时谐波频率增高,滤波相对容易一些,即特定谐波消去法的控制目标是让基波幅值最大,并消除低频次非3倍频次谐波。
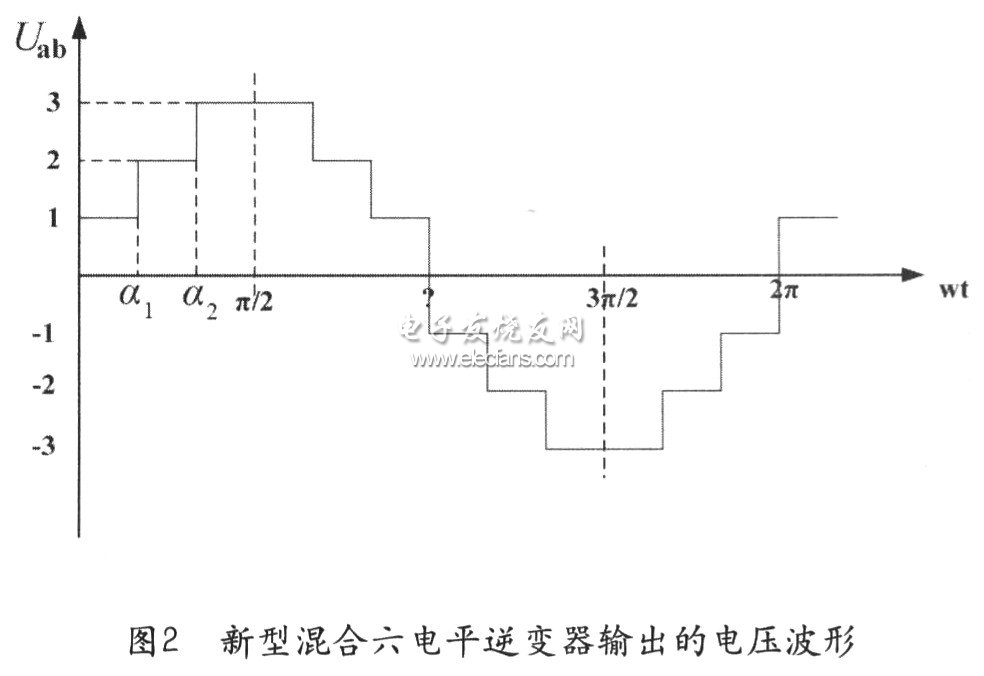
由于图2所示的波形明显满足狄利克雷充分条件,又属于1/4周期对称的波形,所以其傅立叶级数不存在余弦项和所有偶次谐波,于是可得:

式(1)中,Uab(ωt)即是期望输出的粗电压波形。然后将此式展开,表示成如下形式:

称其为调制比,其值的大小决定直流电压利用率的大小。根据式(3),当只有两个开关角时,可以列出以下非线性方程:
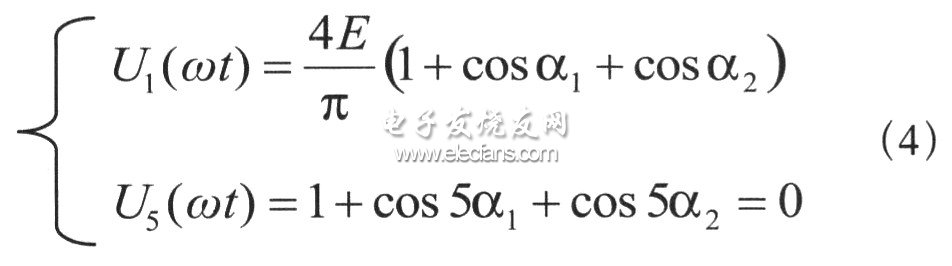
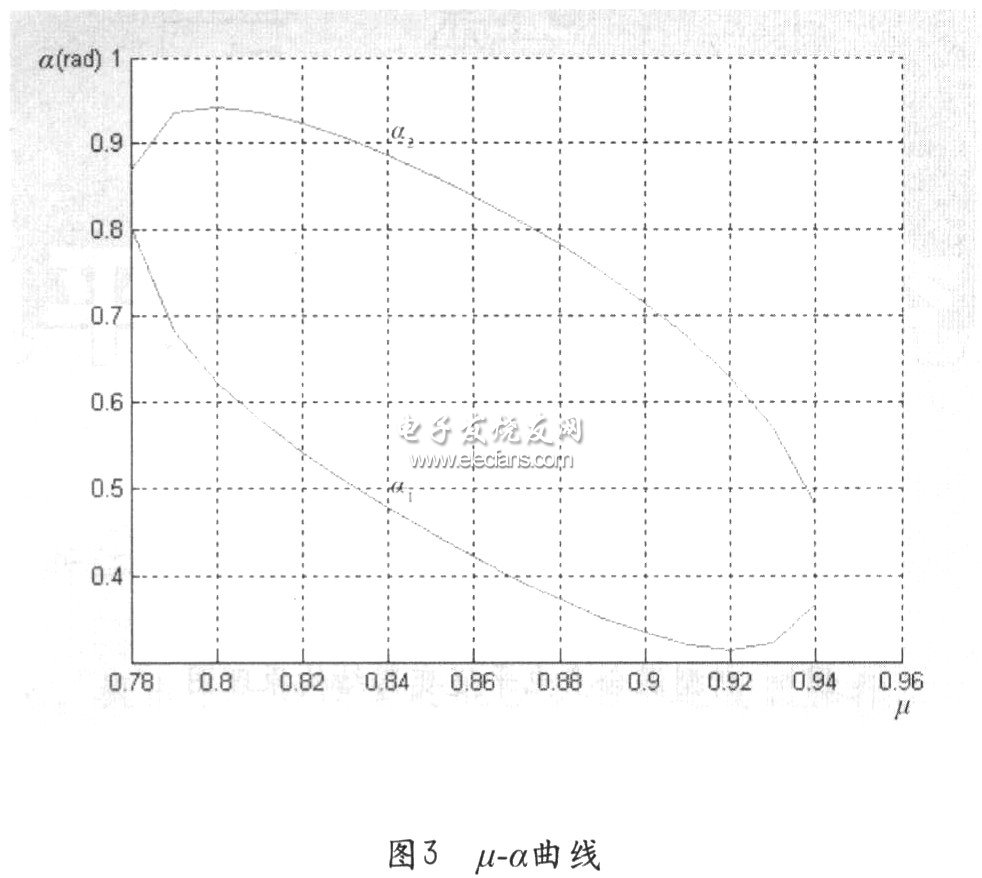
根据式(4),并利用牛顿迭代法,即可解出α1和α2的值,从而实现电路的SHEPWM控制。同时利用MATLAB 7.0中的相关数学工具,解出了不同调制比下的部分α1和α2的值。其μ一α曲线如图3所示。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)